征解问题[11] 解三角形

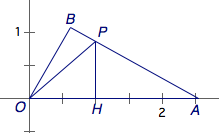
在周长为$6$的三角形$ABO$中，$\angle AOB=60^\circ$，点$P$在边$AB$上，$PH\perp OA$于$H$，且$PH=\dfrac{\sqrt 3}2$，$OP=\dfrac{\sqrt 7}2$，求$OA$．

我的方式是暴力计算．

易得$P\left(1,\dfrac{\sqrt 3}2\right)$，$H(1,0)$．设$A(x,0)$，$B(y,\sqrt 3y)$，则 $$\begin{cases}x+2y+\sqrt{(x-y)^2+3y^2}=6\\\dfrac{\sqrt 3y-0}{y-x}=\dfrac{\dfrac{\sqrt 3}2-0}{1-x}\end{cases}$$

解得