征解问题[9] 二次函数的特殊根（已解决）

题目来自百度贴吧．

已知整系数二次方程$ax^2+bx+c=0$的两个不同实根均在区间$(1,2)$上，求正整数$a$的最小值．

---

 我很快就构造了$a=5$的情形：

根据题目要求，有

$$\begin{cases}a+b+c>0\\4a+2b+c>0\\-\frac{b}{2a}\in (1,2)\\b^2-4ac>0\end{cases}$$

设想一个差不多的方程

$$ax^2-3ax+2a=0,$$ 此时 $$a=a,b=-3a,c=2a.$$ 但该方程的$b$或者$c$需要增大一点，使得 $$a+b+c>0\land 4a+2b+c>0.$$ 但这样会使得判别式失控，我们需要单独处理．

（1）若令$a=a+1$，则有

$$(-3a)^2-4\cdot (a+1)\cdot 2a=a^2-8a>0.$$

（2）若令$b=-3a+1$，则有

$$(-3a+1)^2-4\cdot a\cdot 2a=a^2-6a+1>0.$$

（3）若令$c=2a+1$，则有

$$(-3a)^2-4\cdot a\cdot (2a+1)=a^2-4a>0.$$

看起来方案（3）最科学，于是$a$可以取$5$，此时$b=-15,c=11$，验证通过！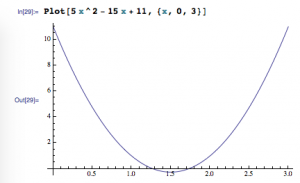

 这样我们构造了$a=5$的情形．

接下来需要说明$a=1,2,3,4$不可能，我是用对称轴和判别式很繁琐的完成这个任务的，大家有更好的方法吗？

---

2015年3月6日更新扒拉题的解法，http://tieba.baidu.com/p/3575904855．

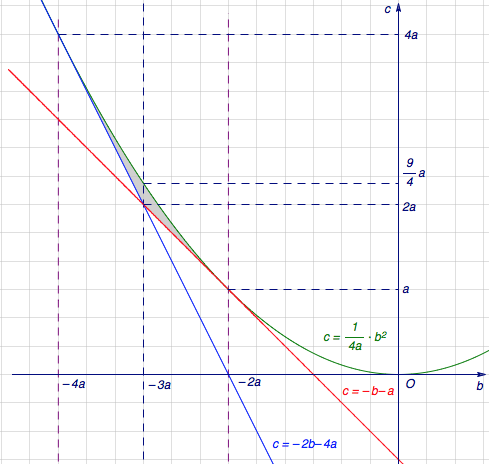
由题意所得的不等式组可以整理为

$$\begin{cases}c>-b-a\\c>-2b-4a\\-4a<b<-2a\\c<\frac{1}{4a}\cdot b^2\end{cases}$$ 其中将$a$看作参数，在坐标系$bOc$中画出可行域

情形1：当$-3a\leqslant b<-2a$时，设$b=-2a-n$，其中$0<n\leqslant a$，$n\in\mathcal Z$．此时

$$-b-a<c<\dfrac{b^2}{4a},$$ 要使该范围内存在整数$c$，需 $$\dfrac{b^2}{4a}-(-b-a)>1$$ 将$b=-2a-n$代入整理得 $$n^2>4a,$$ 要使得在可$0<n\leqslant a$范围内存在整数$n$，只需 $$a^2>4a$$ 解得 $$a>4.$$

情形2：当$-4a<b<-3a$时，设$b=-4a-n$，其中$0<n<a$，$n\in\mathcal Z$．此时

$$-2b-4a<c<\dfrac{b^2}{4a},$$ 要使该范围内存在整数$c$，需 $$\dfrac{b^2}{4a}-(-2b-4a)>1$$ 将$b=-4a-n$代入整理得 $$n^2>4a,$$ 要使得在$0<n<a$范围内存在$n$，只需 $$(a-1)^2>4a,$$ 解得 $$0<a<3-2\sqrt 2\lor a>3+2\sqrt 2.$$

综合情形1与情形2可知，$a\geqslant 5$，进而可以利用情形1构造$a=5$的例子，从略．

---

2015年8月6日更新解法，来源于帷幕讨论组的zhj．

记$f(x)=ax^2+bx+c$，并设两根分别为$x_1$和$x_2$，则

$$f(1)\geqslant 1\land f(2)\geqslant 1,$$ 于是 $$\begin{split}f(1)\cdot f(2)&=a\left(1-x_1\right)\left(1-x_2\right)\cdot a\left(2-x_1\right)\left(2-x_2\right)\\&\leqslant a^2\cdot\left[\dfrac{\left(x_1-1\right)+\left(x_2-1\right)+\left(2-x_1\right)+\left(2-x_2\right)}4\right]^4&=\dfrac{a^2}{16},\end{split}$$ 等号取得的条件为$x_1=x_2=\dfrac 32$，因此可得$a>4$．

令$f(1)=f(2)=1$，$a=5$即得解得$f(x)=5x^2-15x+11$，于是$a$的最小解为$5$．