在$\triangle ABC$中,$AD$是$BC$边上的高.若$BC+AD=AB+AC$,求$\angle BAC$的取值范围.
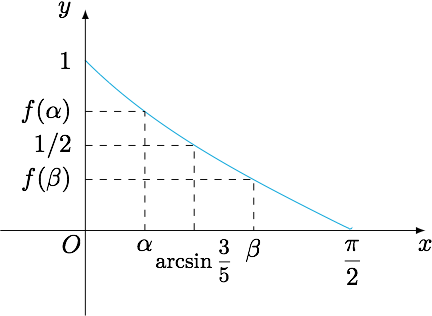
解 显然$D$在边$BC$上,否则$AB+AC>BC+AD$,与题意不符.此时可以把$\angle BAC$看成$\angle BAD$和$\angle CAD$的和,分别设$\angle BAD=\alpha$,$\angle CAD=\beta$,$AD=1$,其中$\alpha$,$\beta$均为锐角,那么有$$\tan\alpha+\tan\beta+1=\dfrac{1}{\cos\alpha}+\dfrac{1}{\cos\beta},$$即$$\dfrac{1-\sin\alpha}{\cos\alpha}+\dfrac{1-\sin\beta}{\cos\beta}=1,$$设$f(x)=\dfrac{1-\sin x}{\cos x}$,那么其导函数为$$f'(x)=\dfrac{\sin x-1}{\cos^2 x},$$其二阶导函数为$$f''(x)=\dfrac{(1-\sin x)^2}{\cos^3 x},$$因此函数$f(x)$为单调递减的下凸函数.从而$$f\left(\dfrac{\alpha+\beta}2\right)\leqslant \dfrac{f(\alpha)+f(\beta)}{2}=\dfrac 12.$$经计算可得$f\left(\arcsin\dfrac 35\right)=\dfrac 12$,因此$$\dfrac{\alpha+\beta}2\geqslant \arcsin\dfrac 35,$$从而$\angle BAC\geqslant 2\arcsin\dfrac 35$.
另一方面,当$\alpha\to 0$,$\beta\to \dfrac{\pi}2$时,$\angle BAC\to \dfrac{\pi}2$,因此$\angle BAC$的取值范围是$\left[2\arcsin\dfrac 35,\dfrac{\pi}2\right)$.
2016年3月20日,来自Brook.
令$AB+AC=BC+AD=2a$,$BC=2c$,$AD=h$,$\angle BAC=\theta$,则由焦点三角形面积公式可得$$\left(a^2-c^2\right)\cdot \tan\dfrac{\theta}2=ch=c(2a-2c),$$整理得$$\tan\dfrac{\theta}2=\dfrac{2}{1+\dfrac ac}.$$又$$0<h=2a-2c\leqslant b,$$于是$$(2a-2c)^2\leqslant a^2-c^2,$$解得$$1<\dfrac ac\leqslant \dfrac 53,$$从而$\tan\dfrac{\theta}2$的取值范围是$\left[\dfrac 34,1\right)$,从而$\theta$的取值范围是$\left[2\arcsin\dfrac 35,\dfrac{\pi}2\right)$.