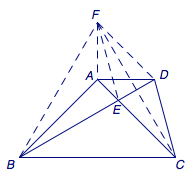
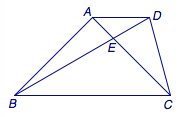
如图,梯形\(ABCD\)中,\(AD\parallel BC\),\(\angle ABD=15^\circ\),\(BC=BD\),\(CD=CE\).求证:三角形\(ABC\)为等腰直角三角形.
我是用三角方法解的,征求纯平面几何方法.
设\(BC=1\),\(\angle CBD=2x\),则\(CD=2\sin x\).
在三角形\(ADC\)中应用正弦定理,有\[\frac{AC}{\sin\angle ADC}=\frac{CD}{\sin\angle CAD},\]于是\[\frac{AC}{\sin\left(x+90^\circ\right)}=\frac{2\sin x}{\sin\left(90^\circ-3x\right)},\]所以\[AC=\frac{\sin 2x}{\cos 3x}.\]
在三角形\(ABC\)中应用正弦定理,有\[\frac{AC}{\sin\angle ABC}=\frac{BC}{\sin\angle BAC},\]于是\[\frac{AC}{\sin\left(2x+15^\circ\right)}=\frac{1}{\sin\left(x+75^\circ\right)},\]整理得\[\frac{\sin 2x}{\sin\left(2x+15^\circ\right)}=\frac{\cos 3x}{\sin\left(x+75^\circ\right)}.\]
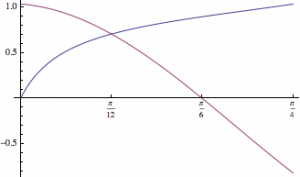
显然,\(0<x<30^\circ\),在此区间左侧单调递增,右侧单调递减(可以由导数证明),因此有唯一实数解\(x=15^\circ\).
进而不难得到三角形\(ABC\)为等腰直角三角形.
我构想的辅助线是这样的: