概率与人们的生活息息相关,有时让我们既入迷又迷惑不解.很多概率问题的结果与我们的直观感受很有出入,比如下面这个问题你直观上感觉有多少?
某种疾病的人群总发病率是\(5\%\),对这种疾病进行机器检测,检测的正确率是\(90\%\),问一个人被诊断患有这种疫病的情况下,确实患有这种疾病的概率是多少?
正确的答案是约为\(32.1\%\).
下面先介绍一个统计模拟的方法让我们从统计角度直观地去理解与感受一下概率.
概率的统计定义是将事件发生的频率近似成概率,当事件不断重复发生时,频率越来越趋近于概率,它的极限便是概率.比如一枚硬币竖直向上抛出,正面朝上的频率会越来越接近\(\dfrac 12\).对于有些概率问题我们可以借助于理想化的统计模型去帮助我们理解概率的公式以及结果.
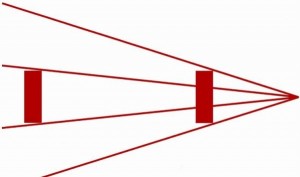
我们先从一个著名的"玛丽莲问题"入手,这个问题是这样的:
台上有三扇门,只有一扇门的背后是汽车,另外两扇门的背后都是山羊.你想选出背后是汽车的那扇门.
你先选择了其中的一扇门(没有打开),这时主持人从剩下的两扇门中打开了一扇背后是山羊的门(主持人事先知道门后面的情况),这时你有一次换门的机会,问:你是保持原来的选择,还是将门换成剩下的那扇?
答案是应该换.
不换门选出汽车的概率是\(\dfrac{1}{3}\),换门后选出汽车的概率是\(\dfrac 23\).
很多人都不信这个结果.我们用统计的方式去模拟一下:
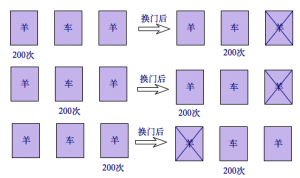
假如你参加了\(600\)次这样的节目,如果不换门,因为你是随机选择的,在统计意义上,可以假定你选择打开每扇门的次数相同,都是\(200\)次,
于是你选出汽车的概率为\(\dfrac 13\),这比较容易理解.
如果你每次都换门呢,情况变成了这样:
这样,选出汽车的次数变成了\(400\)次,概率变成了\(\dfrac 23\).
事实上,原来选中汽车的情况下换门后就不会选出汽车;原来选中羊的情况下,换门后就一定选出汽车.所以选出汽车的概率与原来选出山羊的概率相同.
下面我们来看上面被诊断有病的情况下被"误诊"的概率:我们假设有\(1000\)个人严格符合概率情况,则有下图:
一个人被诊断患病,他有可能是\(95+45=140\)人中的一人,所以它实际患病的概率为\[\dfrac{45}{95+45}\approx 32.1\%.\]这个概率比一般人直观上感觉到的要低.如果总人群的发病率继续降低,比如降到\(2\%\),则检测患病的情况下实际患病的概率会继续下降,只有\(15.5\%\).
从这个意义上来说,有些疾病,如果总体发病率非常低,则初次诊断结果有误的概率还是不小的.当然,如果初次诊断没有患病,那么误诊的概率就很小了.
下面给出一道练习:
有一天晚上一辆出租车肇事逃逸,一个目击者认出那辆车的颜色是蓝色的.已知该城市的绿色出租车有\(85\%\),蓝色出租车有\(15\%\).经测试表明:该目击者可正确辨认颜色的概率是\(80\%\),问肇事车辆确实是蓝色的概率是多少?
正确答案是约等于\(41.4\%\).
注一 误诊概率的问题在数学上可以用贝叶斯公式计算得到结果.
注二 用统计模拟是为了直观地理解概率的计算公式与结果,不能代替计算.