在《2015年高中数学联赛备考手册》的封底发现的:
假设有一个定圆,另有一个半径是定圆半径\(\dfrac{1}{n-1}\)倍的圆在定圆上滚动,则滚动的圆上某定点在滚动时划出的轨迹就是一条外摆线,其方程为\[\begin{cases}x=\cos\theta+\dfrac 1n\cos n\theta,\\y=\sin \theta+\dfrac 1n\sin n\theta.\end{cases}\]
当\(n=2\)时,所得图形是心脏线,著名的分形图案曼德勃罗集正中间的图形就是一个心脏线.
当\(n\)不断增大时,将会形成各式各样的花瓣,你绝对想不到如此复杂多变的图案竟然全部源于一个方程式.



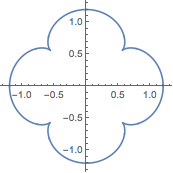
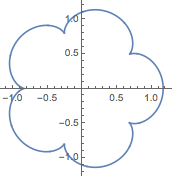
博主用什么软件画的?一直不会用超级画板
Mathematica 10
博主您也看这书啊。这几天牙疼,在医院里一直看这书。
怒赞