我想静静

在《四种典型的动点轨迹问题》中提到“到定点距离等于定长的点的轨迹”问题，但如何从动中找到这个“定点”和“定长”才是关键！

基本图形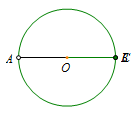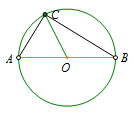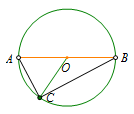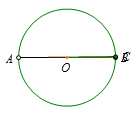直角三角形斜边固定，则它直角顶点在以斜边为直径的圆上．（定点：斜边中点；定长：斜边中线长）

我们先来看个小例子：过定圆内一定点的弦，求这条弦中点的轨迹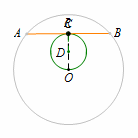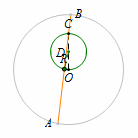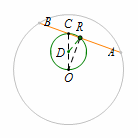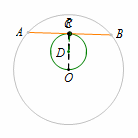．定点：圆心与圆内定点连线的中点$D$；
定长：$DR=\dfrac 12 OC$；
轨迹：以$D$为圆心，$DR$为半径的圆．

例　（浙江湖州中考数学第24（3）题）如图，已知正方形$OABC$的边长为$2$，顶点$A,C$分别在$x,y$轴的正半轴上，$M$是$BC$的中点．$P(0,m)$是线段$OC$上一动点（$C$点除外）．设过$P,M,B$三点的抛物线与$x$轴正半轴交于点$E$，过点$O$作直线$ME$的垂线，垂足为$H$．当点$P$从点$O$向点$C$运动时，点$H$也随之运动，请直接写出点$H$所经过的路径长．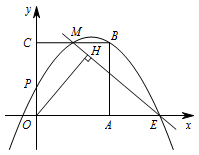

答案　$\dfrac {\sqrt 5}4 \pi$．
分析　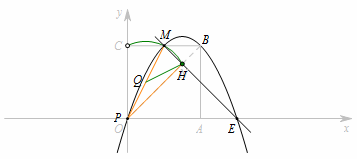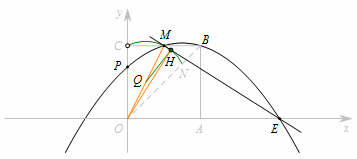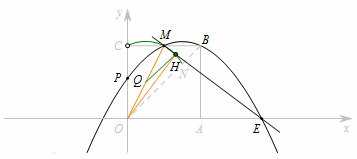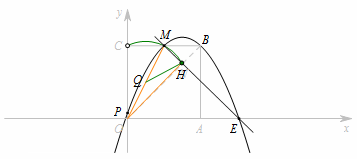定点：$OM$的中点$Q$；
定长：$QH=\dfrac 12OM$；
轨迹：以$Q$为圆心，$QH$为半径的劣弧$CMN$．