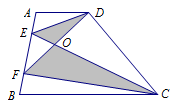
如图，梯形\(ABCD\)中，点\(E,F\)在腰\( AB\)上，\(AE=BF\)，\(CE,DF\)相交于点\(O\)，若梯形\(ABCD\)的面积为\(25\)，\(\triangle OCD\)的面积为\(8\)，则图中阴影部分的面积为_____．
答案 \(9\)．
解析 取\(AB\)中点\(G\)，易得\[S_{\triangle CDG}=\dfrac 12S_{梯形ABCD}.\]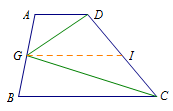
过\(E,F, G\)三点分别作\(CD\)垂线．
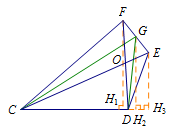因为\[FG=EG,\]所以\[2GH_2=FH_1+EH_3,\]从而\[2S_{\triangle CDG}=S_{\triangle CDE}+S_{\triangle CDF},\]所以\[\begin{split}S_{阴影}&=S_{\triangle CDE}+S_{\triangle CDF}-2S_{\triangle CDO} \\ &=2S_{\triangle CDG}-2S_{\triangle CDO}\\&=9. \end{split}\]
求此问题的关键是怎样将题中已知的梯形的面积进行转换，再结合题中的等线段通过取中点来实现问题的转换．