平面直角坐标系中，\(A(2\sqrt 2,2)\)，点\(Q\)是\(y\)轴上的动点，求\(AQ+\dfrac 13QO\)的最小值．
答案是 \(\dfrac {10}3\)．
解 先构造\(\dfrac 13QO\)，如图，作直线\(l\)，使\[\sin \alpha =\dfrac 13.\]有\[\dfrac 13QO=QH.\]
所以\[AQ+QH\geqslant AH,\]当\(A,Q,H\)三点共线时，线段和取得最小值为\(AH\)．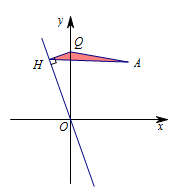
而当\(AH\perp OH\)时，\(AH\)取得最小值．
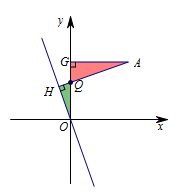作\(AG\perp y\)轴，得\[\triangle AGQ\backsim \triangle OHQ.\]即可求得\(AQ+\dfrac 13QO\)的最小值\(AH\)长为\(\dfrac {10}3\)．
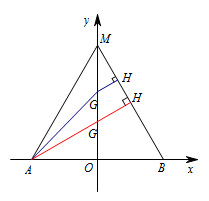
练习 （2009北京中考 25（3）问）如图，在平面直角坐标系中，已知三点\(A(-6,0),B(6,0),M(0,6\sqrt 3)\)，点\(P\)为\(y\)轴上的动点，从\(M\)出发，先沿\(y\)轴到达点\(G\)，再沿\(GA\)到达\(A\)点，若\(P\)点在\(y\)轴上运动的速度是它在直线\(GA\)上运动速度的\(2\)倍，试确定\(G\)的位置，使\(P\)点按照上述要求到达点\(A\)点所用的时间最短．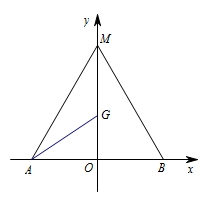
答案是 \(G(0,2\sqrt 3)\)．
解 \(t=\dfrac {MG}{2v}+\dfrac {AG}{v}=\dfrac {1}{v}(\dfrac {MG}{2}+{AG})\)，所以要求时间最短也就是求\((\dfrac {MG}{2}+{AG})\)最小．
因为\[\tan \angle BMO=\dfrac {\sqrt 3}3,\]所以\[ \angle BMO=30^\circ.\]所以\[GH=\dfrac 12 GM.\]即当\(AH\perp MB\)与\(y\)轴交点为\(G\)，此时\(AG+GH\)的值最小．易求\(G(0,2\sqrt 3)\)．