如图，在菱形\(ABCD\)中，\(\angle B=60^\circ\)，\(AB=4\)，点\(E\)在\(BC\)上，\(BE=3CE\)，点\(F\)在\(DE\)上，\(\angle AFC=120^\circ\)，\(EF>EC\)，则\(DF=\)_____．
答案 \(DF=\dfrac 4 7\sqrt{21}\)．
方法一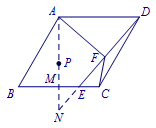
如图，作\(AM\perp BC\)于点\(M\)，延长\(AM\)，\(DE\)，交于点\(N\)， \[\triangle MEN \backsim \triangle ADN,\]所以\[AN=\dfrac{8\sqrt 3}{3},\]
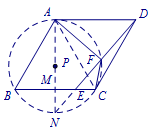由题意可知点\(A\)，\(B\)，\(C\)，\(F\)在同一个\(\odot P\)上， 连接\(AC\)，
因为\(\triangle ABC\)为等边三角形，可得\(\odot P\)的直径为\(\dfrac{8\sqrt 3}{3}\)．
所以\(AN\)为\(\odot P\)的直径．
在\({\rm Rt}\triangle AND\)和\({\rm Rt}\triangle AFD\)中，\[AD^2=DF\cdot DN,\] 所以\[DF=\dfrac 4 7\sqrt{21}.\]
方法二
作\(AO \perp BC\)于\(O\)，以点\(O\)为坐标原点，\(BC\)为\(x\)轴，\(OA\)为\(y\)轴建立直角坐标系．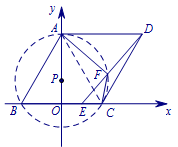 
则\(A(0,2\sqrt 3)\)，\(C(2,0)\)，\(E(1,0)\)，\(D(4,2\sqrt 3)\)，\(P(0,\dfrac{2\sqrt 3}{3})\)．
直线\(ED\)解析式为：\[y=\dfrac{2\sqrt 3}{3}x-\dfrac{2\sqrt 3}{3}.\]设\(F(a,\dfrac{2\sqrt 3}{3}a-\dfrac{2\sqrt 3}{3})\)，由已知得\(PF=PA\)，则
\[a^2+(\dfrac{2\sqrt 3}{3}a-\dfrac{2\sqrt 3}{3}-\dfrac{2\sqrt 3}{3})^2=(\dfrac 43\sqrt 3)^2,\] 解得\(a=\dfrac{16}{7}\)， 所以\(DF=\dfrac 4 7\sqrt{21}\)．