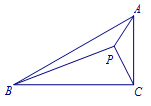
在\(\triangle ABC\)中，\(AB=2AC\)，\(\angle BAC=60^\circ\)，三角形内有一点\(P\)，\(PA=\sqrt 3\)，\(PC=2\)，\(PB=5\)，求\(\triangle ABC \)的面积．
分析 此题刚看到时感觉很像下面这道题（旋转方法）有木有？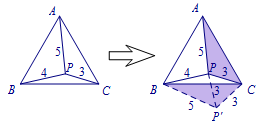
当然我们依然可以用旋转的方法解决．
解 法一 旋转法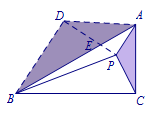
如图，作\(\triangle ADB\)，使得\(\triangle ADB\backsim \triangle APC\)且相似比为\(2:1\)，连接\(DP\)，所以\(\angle DAP=60^\circ\)．
根据已知易得\(\angle ACB=90^\circ\)．
再根据各边长可得到\(\angle APD=90^\circ\)，\(\angle BDP=90^\circ\)，
过\(A\)作\(AM\perp BD\)交\(BD\)延长线于点\(M\)，所以\[AB^2=BM^2+AM^2,\]所以\[\begin{split}S_{\triangle ABC} & =\dfrac 12 AB\cdot AC \sin 60^\circ\\ &=\dfrac{\sqrt 3}{8}AB^2\\ &=\dfrac{6+7\sqrt 3}{2}.\end{split}\]
此题旋转法并不是最简单的方法，由于已知中的角度比较特殊，我们还可以采用更简单的方法来解决．
法二 对称法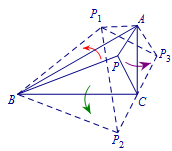
如图，\(P_1\)与\(P\)关于\(AB\)对称，\(P_2\)与\(P\)关于\(BC\)对称，\(P_3\)与\(P\)关于\(AC\)对称．
根据已知易得\(\angle ACB=90^\circ\)，所以\(\angle P_1AP_3=120^\circ\)，\(\angle P_1BP_2=60^\circ\)，
所以\(P_1P_3=3\)，\(P_1P_2=5\)，\(P_2P_3=4\)，
即\(\triangle P_1P_2P_3\)为直角三角形，所以\[S_{\triangle ABC}=\dfrac 12 S_{五边形AP_1BP_2P_3}=\dfrac{6+7\sqrt 3}{2}.\]
除了以上两种方法外，还有一种初中生比较陌生的建立坐标系方法，其实此方法在高中很常用，初中也可以尝试此方法．
法三 坐标系法
根据已知易得\(\angle ACB=90^\circ\)．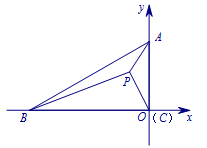
设点\(A(0,x)(x>0)\)，\(P(a,b)\)，则点\(B(-\sqrt 3 x,0)\)．因为\[\begin{cases}a^2+b^2=4,\\(a+\sqrt 3 x)^2+b^2=25,\\a^2+(x-b)^2=3.\end{cases}\]所以\[x^4-14x^2+37=0,\]解得\[x^2=7+2\sqrt 3.\]所以\[S_{\triangle ABC}=\dfrac{\sqrt3}{2}x^2=\dfrac{6+7\sqrt 3}{2}.\]
另：因为点\(P\)在第二象限，所以\(ab<0\)，当\(x^2=7-2\sqrt3\)时，\(ab>0\)，所以舍去；当\(x^2=7+2\sqrt3\)时，\(ab<0\)，符合题意．
总结 当遇见三角形内一点的问题时，若在已知中能找寻到特殊角度，三角形内的点连接各顶点的距离已知时，我们可以采取旋转和对称的方法，建立坐标的方法在初中阶段只了解就可以．