练习题[18] 创新能力培养基础练习

1、已知函数$f(x)=2mx^2-4(4-m)x+1$，$g(x)=mx$，若对于任意实数$x$，$f(x)$与$g(x)$的值至少有一个为正数，则实数$m$的取值范围是_______．

2、已知$x\in\mathcal R$，定义：$\lceil x\rceil$表示不小于$x$的最小整数．若$\lceil 2x+1\rceil=3$，则$x$的取值范围是_______；若$x>0$且$\lceil 2x\cdot \lceil x\rceil\rceil=5$，则$x$的取值范围是_______．

3、$\lim\limits_{x\to 4}{\dfrac{\sqrt{2x+1}-3}{\sqrt x-2}}=$_______．

4、设$\left\{a_n\right\}$满足：$a_{n+1}=\dfrac{1}{4}\left(a_n^4+3\right)$，$a_1>1$．求证：

$$\sum_{n=1}^{\infty}\dfrac{a_n^2+2a_n+3}{\left(a_n+1\right)\left(a_n^2+1\right)}=\dfrac{1}{a_1-1}.$$

5、求证：$\sum\limits_{n=1}^{\infty}{\dfrac{1}{2^n-\dfrac 1{2^n}}}<\dfrac 43$．

6、在三角形$ABC$中，角$A$、$B$、$C$的对边分别为$a$、$b$、$c$，且满足$\left(2a-c\right)\cos B=b\cos C$．

（1）求$B$的大小；

（2）求$\cos^2A+\sin^2C$的最大值．

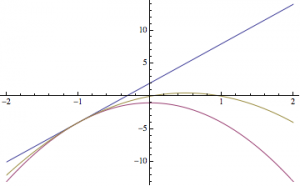
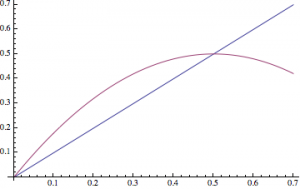
7、设二次函数$y=f(x)$的图象过点$(0,0)$，且满足对任意实数$x$均有

$$-3x^2-1\leqslant f(x)\leqslant 6x+2.$$ 数列$\left\{a_n\right\}$满足：$a_1=\dfrac 13$，$a_{n+1}=f\left(a_n\right)$．

（1）确定$f(x)$的解析式；

（2）求证：$a_{n+1}>a_n$；

（3）求证：$\dfrac{1}{\dfrac 12-a_1}+\dfrac{1}{\dfrac 12-a_2}+\cdots+\dfrac{1}{\dfrac 12-a_n}\geqslant 3^{n+1}-3$．

---

参考答案

1、$(0,8)$．

2、$\left(\dfrac 12,1\right]$；$\left(1,\dfrac 54\right]$．

3、$\dfrac 43$．

提示：令$t=\sqrt x-2$，换元后分子有理化即得．

4、提示：$\dfrac{a_n^2+2a_n+3}{\left(a_n+1\right)\left(a_n^2+1\right)}=\dfrac{1}{a_n-1}-\dfrac{4}{a_n^4-1}=\dfrac{1}{a_n-1}-\dfrac{1}{a_{n+1}-1}$．

5、提示：

$$\dfrac{1}{2^n-\dfrac 1{2^n}}=\dfrac{2^n}{4^n-1}<\dfrac{2^n+1}{4^n}=\dfrac 1{2^n}+\dfrac 1{4^n},$$ 或 $$\dfrac{1}{2^n-\dfrac 1{2^n}}<\dfrac 1{2^{n-1}},$$ 然后后移放缩起点至$n=4$．

6、（1）$B=\dfrac {\pi}{3}$；（2）$1+\dfrac{\sqrt 3}{2}$．

提示：（2）题中代数式变形为

$$\begin{split}\dfrac{1+\cos{2A}}2+\dfrac{1-\cos\left(\dfrac{4\pi}3-2A\right)}{2}&=1+\dfrac{\sqrt 3}4\sin{2A}+\dfrac 34\cos{2A}\\&=1+\dfrac{\sqrt 3}2\sin\left(2A+\dfrac{\pi}{3}\right).\end{split}$$

7、（1）$f(x)=-2x^2+2x$；（2）略；（3）略．

提示：（1）注意到直线$y=6x+2$与抛物线$y=-3x^2-1$相切于$(-1,-4)$，因此$y=f(x)$的图象与此二者的图象亦相切于该点，如图．

 

（2）只需要证明$0<a_n<\dfrac 12$，如图．

 

（3）递推式可以变形为

$$\dfrac 12-a_{n+1}=2\left(\dfrac 12-a_n\right)^2,$$ 而欲证结论可以由 $$\dfrac 12-a_n\leqslant \dfrac{1}{2\cdot 3^n}$$ 推得．