1．(2011年北京市海淀区二模)在正方体$ABCD-A_1B_1C_1D_1$中，$P$为正方形$A_1B_1C_1D_1$四边上的动点，$O$为正方形$ABCD$的中心，$M,N$分别为$AB,BC$的中点，点$Q$为平面$ABCD$内的一点，线段$D_1Q$与$OP$互相平分，则满足$\overrightarrow {MQ}=\lambda\overrightarrow {MN}$的实数$\lambda$的值有_______个．
2．(2009年福建卷)五位同学围成一圈循环报数，规定：
(1) 第一位同学首次报出的数为$1$，第二位同学首次报出的数也为$1$，之后每位同学所报出的数都是前两位同学所报出的数之和；
(2) 若报出的数是$3$的倍数，则该报数的同学需拍手一次．
已知甲同学第一个报数，当五位同学依序循环报到第$100$个数时，甲同学拍手的总数为_______．
3．设函数$f(x)=\dfrac 13x^3-3x^2+(8-a)x-5-a$，若存在唯一的正整数$x_0$，使得$f(x_0)<0$，则$a$的取值范围是_______．
4．设$p,q$为互不相等的正整数，且关于$x$的方程$x^2-px+q=0$和$x^2-qx+p=0$的根都是正整数，则$|p-q|=$_______．
5．已知$x\in\left(0,\dfrac{\pi}2\right)$，求证：
(1) $\sin\left(\sin x\right)<\sin x < \cos \left(\cos x\right)$；
(2) $\sin\left(\cos x\right)<\cos x<\cos\left(\sin x\right)$．
6．求$\left(1+\dfrac 12+\dfrac 13+\cdots +\dfrac 1n\right)^2+\left(\dfrac 12+\dfrac 13+\cdots +\dfrac 1n\right)^2+\cdots +\left(\dfrac 1n\right)^2+\left(1+\dfrac 12+\dfrac 13+\cdots +\dfrac 1n\right)$的值．
7．求证：$2{\rm e}^x>x^3+x^2$．
参考答案
1．$2$．
提示 题意即四边形$OQPD_1$为平行四边形，且$Q$在线段$MN$上．
2．$5$．
先将这五位同学报出的数写成数列：$$a_n:1,1,2,3,5,/8,13,21,35,55,/89,\cdots,$$然后将这个数列各项模$3$的余数写出来：$$\underbrace{1,1,2,0,2,/,2,1,0},\underbrace{1,1,/2,0,2,2,1,/0},\underbrace{1,1,2,0,/2,2,1,0},1,/1,\cdots $$于是我们知道报数遇到数列的第$4k$项时需要拍手．
而甲同学报的数是数列$\{a_n\}$中的第$5n-4(n=1,2,\cdots,20)$项，当$n$是$4$的倍数时，$5n-4$是$4$的倍数，即当$n=4,8,12,16,20$时，甲同学需要报数，因此甲同学拍手的总数为$5$．
3．$\left(\dfrac{1}{15},\dfrac{1}{6}\right]$．
考虑到\[\begin{split} &f_1(a)=\dfrac 13-2a,\\ &f_2(a)=\dfrac 53-3a,\\ &f_3(a)=1-4a,\\ &f_4(a)=\dfrac 13-5a,\\ &f_5(a)=\dfrac 53-6a,\\ &f_6(a)=7-7a,\\ &\cdots \end{split} \]记$f_n(a)=0$的零点为$x_n$，则零点$x_1,x_2,x_3,x_4,x_5$在数轴上分布如图，且容易证明$x_n\geqslant 1$($n\geqslant 6$)（因为$a<\dfrac 16$，所以由$f'(x)=x^2-6x+8-a$知，$f(x)$的极小值点$3+\sqrt{a+1}<5$，所以不需要考虑$n\geqslant 6$的情形）．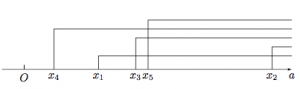
于是当$x_4<a\leqslant x_1$时，$f(x)$存在唯一的正整数$x_0=4$，使得$f(x_0)<0$，此时$a$的取值范围是$\left(\dfrac{1}{15},\dfrac{1}{6}\right]$．
4．设方程$x^2-px+q=0$的两根为$x_1,x_2$，方程$x^2-qx+p=0$的两根为$x_3,x_4$，则$$\begin{cases} x_1+x_2=x_3x_4=p,\\ x_1x_2=x_3+x_4=q.\end{cases} $$
接下来证明$x_1,x_2,x_3,x_4$中必然有至少一个为$1$．否则$x_1,x_2,x_3,x_4\geqslant 2$，此时有$$(x_1-1)(x_2-1)\geqslant 1,(x_3-1)(x_4-1)\geqslant 1,$$即$q\geqslant p$且$p\geqslant q$，于是$p=q$，矛盾．
不妨设$x_1=1$，则$$1+x_3+x_4=x_3x_4,$$从而$$x_3=1+\dfrac{2}{x_4-1},$$于是$$(x_2,x_3,x_4)=(5,3,2),(5,2,3),$$对应的$|p-q|=1$．
5．由三角函数线的定义可得在$\left(0,\dfrac{\pi}2\right)$上$\sin x<x$，而$\dfrac{\pi}2-x\in \left(0,\dfrac{\pi}2\right)$，于是$$\sin\left(\dfrac{\pi}2-x\right)<\dfrac{\pi}2-x,$$即$$x<\dfrac{\pi}2-\cos x.$$这样我们就有在$\left(0,\dfrac{\pi}2\right)$上$$0<\sin x < x <\dfrac{\pi}2-\cos x<\dfrac{\pi}2.$$
(1) 由于函数$y=\sin x$在$\left(0,\dfrac{\pi}2\right)$上单调递增，于是$$\sin(\sin x)<\sin x<\cos(\cos x).$$
(2) 由于函数$y=\cos x$在$\left(0,\dfrac{\pi}2\right)$上单调递减，于是$$\sin(\cos x)<\cos x<\cos (\sin x).$$
6．考虑将$n$个完全平方式展开后的和，包含两部分．第一部分是$$1^2\cdot 1+\dfrac 1{2^2}\cdot 2+\dfrac 1{3^2}\cdot 3+\cdots +\dfrac 1{n^2}\cdot n=1+\dfrac 12+\dfrac 13+\cdots +\dfrac 1n.$$第二部分是\[\begin{split} &2\cdot 1\cdot \left(\dfrac 12+\dfrac 13+\cdots +\dfrac 1n\right)\cdot 1,\\
&2\cdot \dfrac 12\cdot \left(\dfrac 13+\dfrac 14+\cdots +\dfrac 1n\right)\cdot 2,\\
&\cdots \\
&2\cdot \dfrac{1}{n-1}\cdot \dfrac{1}{n}\cdot (n-1),\end{split} \]它们的和为$$2\left[\dfrac 12\cdot 1+\dfrac 13\cdot 2+\cdots +\dfrac 1n\cdot (n-1)\right].$$因此原式的值为$$2\left[1+\dfrac 12\cdot 2+\dfrac 13\cdot 3+\cdots +\dfrac 1n\cdot n\right]=2n.$$
7．考虑证明函数$\varphi(x)={\rm e}^{-x}\cdot \left(x^3+x^2\right)$满足$\varphi(x)<2$．函数$\varphi(x)$的导函数$$f'(x)={\rm e}^{-x}\cdot (-x)\cdot \left[x-\left(1+\sqrt 3\right)\right]\cdot \left[x-\left(1-\sqrt 3\right)\right],$$于是只需要证明$$\varphi\left(1+\sqrt 3\right)<2,\varphi\left(1-\sqrt 3\right)<2,$$即$$\dfrac{14+8\sqrt 3}{{\rm e}^{1+\sqrt 3}}<2,\left(14-8\sqrt3\right)\cdot {\rm e}^{\sqrt 3-1}<2,$$后者显然，而对于前者，我们有$${\rm e}^{1+\sqrt 3}>7+4\sqrt 3\Leftarrow \ln\left(7+4\sqrt 3\right)<\sqrt 3+1,$$而$$\ln \left(7+4\sqrt 3\right)<\ln\left(2{\rm e}^2\right)=2+\ln 2<2+\dfrac{\sqrt 2}2<1+\sqrt 3,$$因此原不等式得证．