1．(2009年北京市崇文区一模)直角坐标系中横坐标和纵坐标均为整数的点称为格点．如果函数$f(x)$的图象恰好通过$k$($k\in\mathcal N^*$)个格点，则称$f(x)$为$k$阶格点函数．下列函数：
(1) $f(x)=\sin x$；
(2) $f(x)=\pi (x-1)^2+3$；
(3) $f(x)=\left(\dfrac 13\right)^x$；
(4) $f(x)={\log_{0.6}}x$．
其中是$1$阶格点函数的有______．
2．(2012年北京市昌平区一模)若对于定义在$\mathcal R$上的函数$f(x)$，其函数图象是连续不断的，且存在常数$\lambda$($\lambda\in\mathcal R$)使得$f(x+\lambda)+\lambda f(x)=0$对于任意实数$x$都成立，则称$f(x)$是一个$\lambda-$伴随函数，有下列关于$\lambda-$伴随函数的结论：
(1) $f(x)=0$是常数函数中唯一一个$\lambda-$伴随函数；
(2) $f(x)=x$不是$\lambda-$伴随函数；
(3) $f(x)=x^2$是一个$\lambda-$伴随函数；
(4) $\dfrac 12-$伴随函数至少有一个零点．
其中正确命题的序号是______ ．
3．设圆$A:(x+1)^2+y^2=1$，圆$B:(x-4)^2+y^2=4$，过圆$B$上一点$M$作圆$A$的切线$MP,MQ$，两条切线分别交$y$轴于$C,D$，则$|CD|$的取值范围是______．
4．正$2016$边形内接于单位圆$O$，从其$2016$个顶点中任选$3$个，设为$A,B,C$，则$\overrightarrow {OA}+\overrightarrow {OB}+\overrightarrow {OC}$的长度不小于$1$的概率为______．
5．已知数列$\{a_n\}$满足$2a_{n+1}=1-a_n^2$，且$0<a_1<1$．求证：当$n\geqslant 3$时，$\left|\dfrac{1}{a_n}-\left(\sqrt 2+1\right)\right|<\dfrac{12}{2^n}$．
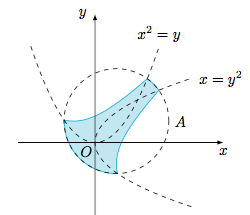
6．圆$O$的半径为$1$，$P$为圆周上一点，现将如图放置的边长为$1$的正方形$ABCD$沿圆周逆时针滚动．假设将正方形的顶点$A$的初始位置记为$P$，当点$A$第一次回到$P$的位置时走过的路径的长度为______．
7．已知点集$A=\left\{(x,y)\mid \left|x-y^2\right|+\left|x^2-y\right|\leqslant 1\right\}$，点集$B=\left\{(x,y)\mid \left(x-\dfrac 12\right)^2+\left(y-\dfrac 12\right)^2\leqslant \dfrac 32\right\}$，求证：$A\subsetneqq B$．
参考答案
1．(1)(2)(4)．
(1) 所有纵坐标为整数的点为$\left(k\pi,0\right)$，$\left(2k\pi+\dfrac{\pi}2,1\right)$，$\left(2k\pi-\dfrac{\pi}2,-1\right)$，其中$k\in\mathcal Z$，因此$f(x)$只通过一个格点$(0,0)$，为$1$阶格点函数．
(2) 通过格点$(1,3)$，且当$x$为除$1$以外的整数时，$f(x)\notin \mathcal Q$，因此$f(x)$为$1$阶格点函数．
(3) 当$x\leqslant 0$且$x\in\mathcal Z$时，$f(x)\in\mathcal Z$，于是$f(x)$通过无数个格点．
(4) 通过格点$(1,0)$，当$x\geqslant 2$且$x\in\mathcal Z$时，$x$不可能是$0.6$的整数次幂．
2．(2)(4)．
(1) $f(x)=C$都是$-1-$伴随函数．
(4) 由于$f\left(x+\dfrac 12\right)+\dfrac 12f(x)=0$，于是在任意区间$\left[x,x+\dfrac 12\right]$上函数$f(x)$必有零点．
3．$\left[\sqrt 2,\dfrac{5\sqrt 2}4\right]$．
设$M\left(4+2\cos\theta,2\sin\theta\right)$，则一方面四边形$MPAQ$的面积$$S=2\cdot \dfrac 12\cdot |AP|\cdot |MP|=\sqrt{|MA|^2-1}=2\sqrt{7+5\cos\theta},$$另一方面又有\[\begin{split} S=&S_{CPAO}+S_{QDOA}+S_{CDM}=&|OA|\cdot|CO|+|OA|\cdot|DO|+\dfrac 12|CD|\cdot |y_M|\\=&\left(3+\cos\theta\right)\cdot |CD|,\end{split}\]于是$$|CD|=\dfrac{2\sqrt {7+5\cos\theta}}{3+\cos\theta},$$令$t=\sqrt{7+5\cos\theta}$，$t\in\left[\sqrt 2,2\sqrt 3\right]$，则有$$|CD|=\dfrac{10t}{8+t^2}=\dfrac{10}{t+\dfrac 8t},$$其取值范围是$\left[\sqrt 2,\dfrac{5\sqrt 2}4\right]$．
4．$\dfrac{1512}{2015}$．
不妨设$A\left(1,0\right)$，$B\left(\cos\alpha,\sin\alpha\right)$，$C\left(\cos\beta,\sin\beta\right)$，其中$\alpha=x\cdot \dfrac{2\pi}{2016}$，$\beta=y\cdot\dfrac{2\pi}{2016}$，$x,y\leqslant 2015$，$x,y\in\mathcal N^*$且$x\neq y$．总样本空间为$2015\times 2014$，且根据题意，有\[\begin{split} \left|\overrightarrow {OA}+\overrightarrow {OB}+\overrightarrow {OC}\right|^2-1&=\left(1+\cos\alpha+\cos\beta\right)^2+\left(\sin\alpha+\sin\beta\right)^2-1\\&=2+2\cos\alpha+2\cos\beta+2\cos\left(\alpha-\beta\right)\\&=4\cos\dfrac{\alpha+\beta}2\cos\dfrac{\alpha-\beta}2+4\cos^2\dfrac{\alpha-\beta}2\\&=4\cos\dfrac{\alpha-\beta}2\left[\cos\dfrac{\alpha+\beta}2+\cos\dfrac{\alpha-\beta}2\right]\\
&=8\cos\dfrac{\alpha-\beta}2\cos\dfrac{\alpha}2\cos\dfrac{\beta}2\\&\geqslant 0
.\end{split} \]情形一 $0<\alpha,\beta< {\pi}$，此时$1\leqslant x,y\leqslant 1007$，共有${\rm A}_{1007}^2$个基本事件符合题意．
情形二 ${\pi}< \alpha,\beta<2{\pi}$，此时$1009\leqslant x,y\leqslant 2015$，共有${\rm A}_{1007}^2$个基本事件符合题意．
情形三 $\alpha=\pi$或$\beta=\pi$，此时$x=1008$或$y=1008$，共有$4028$个基本事件符合题意．
情形四 $\alpha$和$\beta$分别位于$\left(0,\pi\right)$和$\left(\pi,2\pi\right)$，此时$\left|\alpha-\beta\right|>\pi$，即$|x-y|\geqslant 1008$，共有$2{\rm C}_{1008}^2$个基本事件符合题意．
综上所述，所求的概率为$$\dfrac{2{\rm A}_{1007}^2+2{\rm C}_{1008}^2+4028}{2015\times 2014}=\dfrac{1512}{2015}.$$
5．设迭代函数$f(x)=\dfrac 12\left(1-x^2\right)$，那么函数的不动点为$x=\sqrt 2-1$，一个保值区间是$\left[0,\dfrac 12\right]$．
考虑到$0<a_1<1$，于是$0<a_2<\dfrac 12$，从而$\dfrac 38<a_3<\dfrac 12$．
由不动点改造递推数列得$$|a_{n+1}-(\sqrt 2-1)|=\dfrac 12|a_n-(\sqrt 2-1)|\cdot|a_n+\sqrt 2-1|<\dfrac 12|a_n-(\sqrt 2-1)|,$$又当$n=3$时，$|a_3-(\sqrt 2-1)|<\dfrac 18$，于是当$n\geqslant 3$时，有$$\left|a_n-\left(\sqrt 2-1\right)\right|<\dfrac{1}{2^n}.$$而欲证明不等式即$$\left|\dfrac{\left(\sqrt 2-1\right)-a_n}{a_n\left(\sqrt 2-1\right)}\right|<\dfrac{12}{2^n},$$于是只需要证明$$\left|a_n\left(\sqrt 2-1\right)\right|>\dfrac{1}{12},$$也即$$a_n>\dfrac{\sqrt 2+1}{12},n\geqslant 3.$$事实上，当$n\geqslant 3$时，有$$a_n>\dfrac 38>\dfrac{\sqrt 2+1}{12},$$于是原命题得证．
6．每次转动的角均为$\dfrac{\pi}6$，而半径分别为$1,\sqrt 2,1,0,\cdots $，因此所求的路径总长为$$3\cdot\dfrac{\pi}6\cdot\left(1+\sqrt 2+1\right)=\dfrac{\left(2+\sqrt 2\right)\pi}2.$$
7．点集$B$即圆$x^2+y^2-x-y=1$的内部(包含边界)，而$$1\geqslant \left|x-y^2\right|+\left|x^2-y\right|\geqslant \left|\left(x-y^2\right)-\left(x^2-y\right)\right|=\left|x^2+y^2-x-y\right|,$$于是$A\subseteq B$．
另一方面，点$P\left(\dfrac 12,\sqrt{\dfrac 32}+\dfrac 12\right)\in B$，但点$P\notin A$，于是$A\neq B$．
综上所述，$A\subsetneqq B$．
注 事实上，点集$A$如图所示．