1、若$a,b,x,y\in\mathcal R$,$3a+4b=12$,$(x-1)^2+y^2=2$,则$|x-a|+|y-b|$的最小值是_______.
2、已知$f(x)$是定义在$[a,b]$上的函数,如果存在常数$M>0$,对区间$[a,b]$的任意划分:$$a=x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b,$$和式$$|f(x_0)-f(x_1)|+|f(x_1)-f(x_2)|+\cdots +|f(x_{n-1})-f(x_n)|\leqslant M$$恒成立,则称$f(x)$为$[a,b]$的“有限振荡函数”.现有下列四个命题:
① 函数$f(x)=\sin x+\cos x$是$\left[-\dfrac{\pi}2,0\right]$上的“有限振荡函数”;
② 函数$f(x)=\begin{cases} 0,x=0,\\ x\cos\dfrac{\pi}{2x},0<x\leqslant 1,\end{cases} $是$[0,1]$上的“有限振荡函数”;
③ 若函数$f(x),g(x)$都是$[a,b]$上的“有限振荡函数”,则$f(x)+g(x)$也是$[a,b]$上的“有限振荡函数”;
④ 存在常数$k>0$,使得对任意$x_1,x_2\in [a,b]$,均有$$|f(x_1)-f(x_2)|\leqslant k|x_1-x_2|,$$则$f(x)$为$[a,b]$上的“有限振荡函数”,反之亦然.
其中所有正确的命题是_______.
3、函数$f(x)={\rm e}^{ax}-\dfrac 1a\ln x$存在零点,则$a$的取值范围是_______.
4、设$[x]$为$x$的整数部分,则$\left[\dfrac{10^{20000}}{10^{100}+3}\right]$的个位数字是_______.
5、已知$\alpha,\beta,\gamma$均为锐角,且$$\cos^2\alpha +\cos^2\beta+\cos^2\gamma =1,$$求证:$\dfrac{3\pi}4<\alpha+\beta+\gamma<\pi$.
6、求证:$x^2{\rm e}^x-\ln x>1$.(参考数据:$\ln 2\approx 0.693$,$\sqrt{\rm e}\approx 1.649$.)
7、已知$x>0$,求$\sqrt{\dfrac{1}{1+x^2}}+2\sqrt{\dfrac{x}{1+x}}$的最大值.
参考答案
1、$\dfrac{9-5\sqrt 2}4$
2、①③④
3、$(-\infty,0)\cup (0,{\rm e}^{-1}]$
4、$3$
提示 $\left[\dfrac{10^{20000}}{10^{100}+3}\right]=\dfrac{(10^{100})^{200}-3^{200}}{10^{100}+3}$.
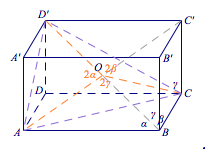
5、提示 构造长方体的对角线,在三面角中证明.如图:
取长方体的中心$O$,不妨设$$\angle ABD'=\alpha ,\angle CBD'=\beta,\angle B'BD'=\gamma,$$连接$BD$,则有$$\alpha=\angle D'BA>\angle DBA,\beta=\angle D'BC>\angle DBC,$$于是有$\alpha+\beta>\dfrac {\pi}{2}$,从而不等式左边得证;
由$OA=OC'=OB=OD'=OC$知$$\angle AOD'=2\alpha,\angle COD'=2\beta,\angle AOC=2\gamma.$$事实上,$O$为三棱锥$O-ACD'$的顶点,且$O$在底面$ACD'$上的投影为底面外心,与证明不等式左边的方法类似可以得到$$2\alpha+2\beta+2\gamma<2\pi,$$不等式右边得证.
代数方法(由meiyun提供)
由题中等式得$$\cos^2\gamma=-\dfrac 12(\cos{2\alpha}+\cos{2\beta})=-\cos(\alpha+\beta)\cos(\alpha-\beta)>0,$$从而有$$\alpha+\beta>\dfrac {\pi}{2},$$$\alpha,\beta,\gamma$位置关系一样,从而得到不等式左边.
下面用反证法证明不等式右边:
不妨设$\alpha\geqslant \beta\geqslant \gamma$,若$\alpha+\beta+\gamma\geqslant \pi$,则有$$0<\pi-\alpha-\beta\leqslant \gamma,$$从而有$$\cos^2\gamma=\cos(\pi-\alpha-\beta)\cos(\alpha-\beta)\geqslant \cos{\gamma}\cos(\alpha-\beta),$$于是有$\cos\gamma>\cos(\alpha-\beta)$,从而$\gamma<\alpha-\beta$,于是$$\pi\leqslant\alpha+\beta+\gamma<2\alpha,$$与$\alpha$为锐角矛盾.
6、由于在$x>0$时,$(x^2{\rm e}^x)'={\rm e}^x(x^2+2x)$单调递增,而$(\ln x)'=\dfrac 1x$单调递减,于是$$x^2{\rm e}^x\geqslant \dfrac{5\sqrt{\rm e}}4\left(x-\dfrac 12\right)+\dfrac{\sqrt{\rm e}}4,$$且$$\ln x\leqslant 2\left(x-\dfrac 12\right)+\ln\dfrac 12,$$两式相减可得$$x^2{\rm e}^x-\ln x\geqslant \left(\dfrac{5\sqrt{\rm e}}4-2\right)x-\dfrac{3\sqrt{\rm e}}8+1+\ln 2,$$由于$$\dfrac{5\sqrt{\rm e}}4-2>0,$$于是$$x^2{\rm e}^x-\ln x>-\dfrac{3\sqrt{\rm e}}8+1+\ln 2>1.07>1,$$因此原不等式得证.
另法
由于${\rm e}^x\geqslant {\rm e}x$,于是$$x^2{\rm e}^x-\ln x\geqslant {\rm e}x^3-\ln x,$$记右侧函数为$f(x)$,则$$f'(x)=\dfrac{3{\rm e}x^3-1}{x},$$于是$f(x)$的最小值为$$f\left((3{\rm e})^{-\frac 13}\right)=\dfrac 23+\dfrac 13\ln 3>1,$$因此原不等式得证.
7、设所求代数式为$f(x)$,则$f(x)$的导函数$$f'(x)=\dfrac{(1+x^2)^{\frac 32}-(x+x^2)^{\frac 32}}{\sqrt x\cdot (1+x)^{\frac 32}\cdot (1+x^2)^{\frac 32}},$$于是函数$f(x)$在$(0,1)$上单调递增,在$(1,+\infty)$上单调递减,因此所求最大值为$$f(1)=\dfrac{3}{\sqrt 2}.$$