1、椭圆$C$的两个焦点分别为$F_1,F_2$,椭圆$C$上恰好有$6$个不同的点$P$使得$\triangle PF_1F_2$为等腰三角形,则椭圆$C$的离心率的取值范围是_______.
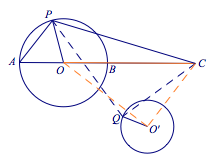
2、已知$P$是以$AB$为直径的圆$O$上一点,且$B$是线段$AC$的中点,$AB=10$.以$CP$为斜边作直角三角形$QPC$,且$\tan\angle QPC=\dfrac 34$,则线段$OQ$的最小值是_______.
3、已知函数$f(x)=x^3+bx+c$有两个零点$n,m$且满足$f'(m)=0$,$0<m-n<1$.则函数$$g(x)=\dfrac 13x^3-\dfrac 32x^2+(b+2)x+(c-b+n)\ln x+d$$在$(n+1,m+1)$上( )
A.有且只有一个零点
B.至多只有一个零点
C.可能有两个零点
D.以上说法均不正确
4、函数$f(x)=ax^2+bx+c$($a>0,b,c\in\mathcal R$)的图象过$(1,0)$,且在区间$[0,2]$上的最大值与最小值之和大于$\dfrac 32a$,则$\dfrac ba$的取值范围是_______.
5、在$\triangle ABC$中,$AC=2$,$D$为$AC$的中点,$\angle A=\angle CBD=2\angle ABD$,则$\triangle ABC$的面积为_______.
6、在平面直角坐标系$xOy$中,圆$M:(x-a)^2+(y+a-3)^2=1$($a>0$),点$N$为圆$M$上任意一点.若以$N$为圆心,$ON$为半径的圆与圆$M$至多只有一个公共点,则$a$的最小值为_______.
7、已知$x,y,z>0$且$xyz=\dfrac 12$,$x^2+y^2+z^2\leqslant 2$,求$x^4+y^4+z^4$的最大值.
参考答案
1、$\left(\dfrac 13,\dfrac 12\right)\cup\left(\dfrac 12,1\right)$
2、$9$
提示 $Q$在圆上运动,设圆心为$O'$,则$\triangle POC$与$\triangle QO'C$旋转相似.
3、B
提示 $n=-2m$,$b=-3m^2$,$c=2m^3$,$g'(n+1)=0$,故$g'(x)$可以因式分解 $$g'(x)=\dfrac {(x+2m-1)(x-m)(x-m-2)}{x},$$而$x\in (1-2m,m+1)$,所以$g(x)$单调递减.
4、$(-\infty,-4+\sqrt 2)\cup (-\sqrt 2,+\infty)$
5、$\dfrac{\sqrt 3+1}2$
6、$3$
提示 圆心$M$在直线$y=-x+3$上运动,当两个圆内切时为临界状态.
7、显然,当$x^2+y^2+z^2=2$时原式取得最大值.此时$$y^2+z^2=2-x^2\geqslant 2yz=\dfrac 1x,$$从而解得$$\dfrac{\sqrt 5-1}2\leqslant x\leqslant 1,$$不妨设$x\geqslant y\geqslant z$,则有$$\sqrt{\dfrac 23}\leqslant x\leqslant 1.$$
另一方面,有$$x^4+y^4+z^4=x^4+(y^2+z^2)^2-2y^2z^2=2x^4-4x^2+4-\dfrac{1}{2x^2},$$设$RHS=f(x)$,则其导函数$$f'(x)=\dfrac{8x^6-8x^4+1}{x^3},$$于是分子部分的导函数为$$16x^3(3x^2-2),$$不难推得函数$f(x)$在$\left[\sqrt{\dfrac 23},1\right]$上先递减再递增,因此函数$f(x)$的最大值在区间端点处取得,不难计算得当$x=1$时,$f(x)$最大,为$\dfrac 32$.
综上,当$(x,y,z)=\left(1,\dfrac{\sqrt 2}2,\dfrac{\sqrt 2}2\right)$或其轮换时,$x^4+y^4+z^4$取得最大值为$\dfrac 32$.