1、已知函数$f(x)=x^2$与$g(x)=a(x-1)$的图象有两个交点，其横坐标$x_1=\sin\alpha$，$x_2=\cos\alpha$，则$x_1^3+x_2^3=$_______．
2、在三角形$ABC$中，$AB$边上的中线$CO=2$，若动点$P$满足$\overrightarrow {AP}=\sin^2\theta \cdot\overrightarrow {AO}+\cos^2\theta\cdot\overrightarrow {AC}$（$\theta\in \mathcal R$），求$\left(\overrightarrow {PA}+\overrightarrow {PB}\right)\cdot\overrightarrow {PC}$的最小值．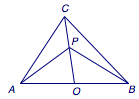 
3、已知向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$满足$\left| \overrightarrow a\right|=\left|\overrightarrow b\right|=2$，$\left|\overrightarrow c\right|=1$，$\overrightarrow a\cdot \overrightarrow b=2$，则$\left(\overrightarrow a-\overrightarrow c\right)\cdot\left(\overrightarrow b-\overrightarrow c\right)$的最大值为_______．
4、已知函数$f(x)=x^2+ax+b$，存在不为$0$的实数\(t\)，使得$f(t)+f\left(\dfrac 1t\right)=-2$，则$a^2+4b^2$的最小值是_______．
5、已知$f(x)$是定义在$\mathcal{R}$上的可导函数，且对任意$x>0$，都有$f(x)>0$．若对任意$x>0$，均有$f(x)>f'(x)\cdot\ln x^x$，则$f(2)$与$f({\rm e} )\cdot \ln 2$的大小关系是_______．
6、已知实数$x,y$满足条件$$\begin{cases} x-y\leqslant 0,\\x+y-5 \geqslant 0,\\ y-3\leqslant 0.\end{cases} $$若不等式$m(x^2+y^2)\leqslant (x+y)^2$恒成立，则实数$m$的取值范围是_______．
7、已知双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（$a,b>0$）的左、右焦点分别为$F_1$、$F_2$，焦距为$6$，过右焦点$F_2$向其中一条渐近线作垂线$F_2H$，交渐近线于$H$，则$\triangle F_1F_2H$周长的最大值为_______．
参考答案
1、$\sqrt 2-2$ $x_1$、$x_2$是方程$$x^2-ax+a=0$$的两根，进而可以由$$x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1\cdot x_2=1$$解得$$a=1-\sqrt 2,$$于是$$x_1^3+x_2^3=(x_1+x_2)^3-3x_1x_2(x_1+x_2)=\sqrt 2-2.$$
2、注意到$$\overrightarrow {AP}=\lambda\overrightarrow {AO}+(1-\lambda)\overrightarrow {AC},$$其中$\lambda =\sin^2\theta\in [0,1]$，于是点$P$在线段$CO$上（包括两个端点），且$\overrightarrow {CP}=\lambda \overrightarrow {CO}$．
运用向量的换底公式，将起点统一为$C$，有$$\begin{split} \left(\overrightarrow {PA}+\overrightarrow {PB}\right)\cdot\overrightarrow {PC}&=\left(\overrightarrow {CA}-\overrightarrow {CP}+\overrightarrow {CB}-\overrightarrow {CP}\right)\cdot\left(-\overrightarrow {CP}\right)\\&=\left[2 \overrightarrow {CP}-\left(\overrightarrow {CA}+\overrightarrow {CB}\right)\right]\cdot\overrightarrow {CP}\\&=\left(2\overrightarrow {CP}-2\overrightarrow{CO}\right)\cdot\overrightarrow {CP}\\&=2 \overrightarrow {CP}\cdot\overrightarrow {CP}-2\cdot \overrightarrow {CO}\cdot\overrightarrow {CP}\\&=8\lambda^2-8\lambda, \end{split} $$又$\lambda \in[0,1]$，于是所求的最小值为$-2$，当$\lambda = \dfrac 12$，也即$\sin^2\theta=\dfrac 12$时取得．
3、$3+2\sqrt 3$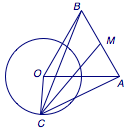 
如图，$OA=OB=2$，$\angle AOB=60^\circ$，圆的半径为$1$，点$C$在圆上运动，则问题转化为求$\overrightarrow {CA}\cdot\overrightarrow {CB}$的最大值． 由极化恒等式，可得$$\overrightarrow {CA}\cdot\overrightarrow {CB}=CM^2-\dfrac 14AB^2,$$于是当$CM$最大，即$CM=OM+OC=\sqrt 3+1$时，$\overrightarrow {CA}\cdot\overrightarrow {CB}$取得最大值，为$3+2\sqrt 3$．
4、$\dfrac{16}5$ 根据题意有$$\left(t+\dfrac 1t\right)\cdot a+2b+\left( t+\dfrac 1t\right)^2=0,$$于是点$(a,2b)$是直线$$\left(t+\dfrac 1t\right)\cdot x+y+\left( t+\dfrac 1t\right)^2=0$$上的点，于是点$(a,2b)$到原点的距离不小于原点到此直线的距离，即$$\sqrt{a^2+4b^2}\geqslant \dfrac{\left| \left(t+\dfrac 1t\right)^2 \right| }{\sqrt{1^2+\left(t+\dfrac 1t\right)^2}},$$令$m=\left|t+\dfrac 1t\right|$，则$m \geqslant 2$，且$$a^2+4b^2\geqslant \dfrac{m^4}{m^2+1}\geqslant \dfrac{16}5.$$ 注 本题也可以用柯西不等式进行转化．
5、$f(2)>f({\rm e} )\cdot\ln 2$．
提示：考虑函数$\dfrac{f(x)}{\ln x}$．
6、$\left[\dfrac{25}{13},2\right]$
提示：可以将代数式$\dfrac{(x+y)^2}{x^2+y^2}$转化成关于\(\dfrac yx\)的函数，从而求出最值．
7、$4\sqrt 3+6$ 根据题意，$a^2+b^2=9$，且$$\cos \angle HF_2F_1=\sin \angle HOF_2=\dfrac b3,$$于是$$\begin{split} F_1H+F_2H&=\sqrt{b^2+6^2-2\cdot b\cdot 6\cdot \dfrac b3}+b\\&=\sqrt{36-3b^2}+b\\&=\sqrt 3\cdot\sqrt{12-b^2}+1\cdot b\\&\leqslant 4\sqrt 3, \end{split} $$于是$ \triangle F_1F_2H$周长的最大值为$4\sqrt 3+6$．