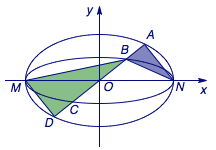
1、如图,已知椭圆\(C_1\)与\(C_2\)的中心在坐标原点\(O\),长轴均为\(MN\)且在\(x\)轴上,短轴长分别为\(2m\)、\(2n\)(\(m>n\)),过原点且不与\(x\)轴重合的直线\(l\)与\(C_1\),\(C_2\)的四个交点按纵坐标从小到大依次为\(A,B,C,D\).记\(\lambda=m/n\),三角形\(BDM\)和三角形\(ABN\)的面积分别为\(S_1\),\(S_2\).
(1)当直线\(l\)与\(y\)轴重合时,若\(S_1=\lambda S_2\),求\(\lambda\)的值;
(2)当\(\lambda\)变化时,是否存在与坐标轴不重合的直线\(l\)使得\(S_1=\lambda S_2\)?说明理由.
2、已知函数\(f(x)=ax^2-4\ln (x-1)\),\(a\in\mathcal R\).
(1)当\(a=1\)时,求\(f(x)\)的单调区间;
(2)已知点\(P(1,1)\)和函数\(f(x)\)图象上的动点\(M(m,f(m))\),对任意\(m\in [2,\mathcal e+1]\),直线\(PM\)的倾斜角都是钝角,求\(a\)的取值范围.
3、设无穷等比数列\(\{a_n\}\)的公比为\(q\),且\(a_n>0(n\in\mathcal N^*)\),\([a_n]\)表示不超过实数\(a_n\)的最大整数(如\([2.5]=2\)),记\(b_n=[a_n]\),数列\(\{a_n\}\)的前\(n\)项和为\(S_n\),数列\(\{b_n\}\)的前\(n\)项和为\(T_n\).
(1)若\(a_1=4\),\(q=\dfrac 12\),求\(T_n\);
(2)若对于任意不超过\(2014\)的正整数\(n\)都有\(T_n=2n+1\),证明:\[\left(\dfrac 23\right)^{\frac 1{2012}}<q<1;\]
(3)证明:\(S_n=T_n\)(\(n=1,2,\cdots\))的充分必要条件是\(a_1\in\mathcal N^*\),\(q\in\mathcal N^*\).
参考答案
1、(1)\(1+\sqrt 2\);(2)当\(\lambda\in\left(1,1+\sqrt 2\right]\)时不存在,当\(\lambda\in\left(1+\sqrt 2,+\infty\right)\)时存在.
提示:(2)\(\dfrac{S_1}{S_2}\)与\(A,B\)点横坐标的比单调变化,而\(A,B\)点横坐标的比与\(k\)单调变化,从而可以求出\(\dfrac{S_1}{S_2}\)的范围是\(\left(\dfrac{m+n}{m-n},+\infty\right)\).
2、(1)\(f(x)\)的单调递增区间为\((2,+\infty)\),单调递减区间为\((1,2)\);
(2)\(a\)的取值范围是\(\left(-\infty,\dfrac 14\right)\).
提示:(2)可以分离变量求解.
3、(1)列举可得\[T_n=\begin{cases}4,&n=1\\6,&n=2\\7,&n\geqslant 3\end{cases}\]
(2)提示:\(a_1\in [3,4)\),\(a_2,a_3,\cdots,a_{2014}\in [2,3)\).
(3)提示:\(a_n=b_n\),用反证法,利用有理数的性质推出矛盾.