2015年江苏省盐城市三模理科数学第14题:
若函数\(f(x)=-\ln x+ax^2+bx-a-2b\)有两个极值点\(x_1,x_2\),其中\(-\dfrac 12<a<0<b\),且\(f\left(x_2\right)=x_2>x_1\),则方程\(2a\left[f(x)\right]^2+bf(x)-1=0\)的实根个数为_______.
正确的答案是\(5\)个.
解 函数\(f(x)\)的导函数\[f'(x)=\dfrac{2ax^2+bx-1}x,\]于是方程\[2a\left[f(x)\right]^2+bf(x)-1=0\]的实根实际上就是复合函数\(f'\left(f(x)\right)\)的零点,其处理方法是从外向内逐层“剥开”.
根据以上分析,题中方程等价于\[f(x)=x_1\lor f(x)=x_2,\]因此其实根个数就是函数\(f(x)\)的图象与直线\(y=x_1\)以及直线\(y=x_2\)的交点个数的总和.这样一来,如何准确做出函数\(f(x)\)的图象成了解决问题的关键.
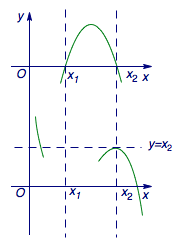
如图,由\(a<0\)可以作出\(f'(x)\)的“示性函数”(决定函数值正负性质的部分因式)\(y=2ax^2+bx-1\)的草图.又函数\(f(x)\)的定义域为\((0,+\infty)\),其在区间端点处的函数值\(f(0+)=+\infty\),\(f(+\infty)=-\infty\).此外题中告知\(f\left(x_2\right)=x_2>0\).
结合导函数图象与函数在\(0\)、\(x_2\)、\(+\infty\)处的取值可以作出函数\(f(x)\)的部分图象(缺失极值点\(x=x_1\)处的信息).据此“残图”可以确定直线\(y=x_2\)与函数\(f(x)\)的图象交点数为\(2\).
为了确定函数\(f(x)\)的图象中残缺的部分,我们需要另外探寻一些特殊点.先考虑方程\[2ax^2+bx-1=0,\]有\[x_1+x_2=-\dfrac b{2a}\land x_1x_2=-\dfrac{1}{2a},\]进而可得\[x_1+x_2\in\left(0,+\infty\right)\land x_1x_2\in\left(1,+\infty\right),\]这样一来,我们可以断定\(x_2>1\),因此选择\(x=1\)为特殊点进行探索.
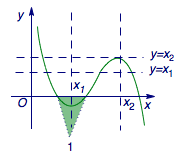
事实上,\(f(1)=-b<0\),于是我们“勘探”出在\(x=x_2\)左侧的未知领域有一片“绿洲”(函数值小于\(0\)的部分),而\(x=x_1\)就是这片绿洲的中心小镇.这样就有\(x_1>0>f\left(x_1\right)\),如图.这样直线\(y=x_1\)与函数\(y=f(x)\)的图象有\(3\)个交点.
综上,题中方程的实根个数为\(5\).
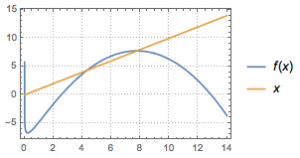
最后给出一个近似准确的图象,其中\(a=-0.3\),\(b=4.788\).
注一 此类函数的零点问题在《函数的零点问题小结》一文中亦有提及.
注二 关于如何正确的画函数图形,可以参考《每日一题[261]画图也要有诀窍》.
注三 菁优网给出的解答(其中有漏洞):
http://www.jyeoo.com/math2/ques/detail/c61521a9-26e5-40ad-a722-c15d718391ce.