每日一题[25] 复合函数的“组合图象”

讨论某个含参方程的根的个数是高中数学函数模块中经常遇到的问题．这类题一般通过将方程的解看做是两个函数的图象交点的横坐标来解决，其本质为将一维的方程的根的问题升到二维的函数图象的交点问题．这就好比是如果想搞清楚某个城市的道路情况，从空中鸟瞰往往比遍历一遍这个城市效率高得多．接下来，我们一起欣赏一道小题．

 讨论关于$x$的方程

$$\left(x^2-1\right)^2-2\left|x^2-1\right|+k=0$$ 的根的个数．

---

原方程的根的个数即函数$y=-\left(x^2-1\right)^2+2\left|x^2-1\right|$与直线$y=k$的交点个数．

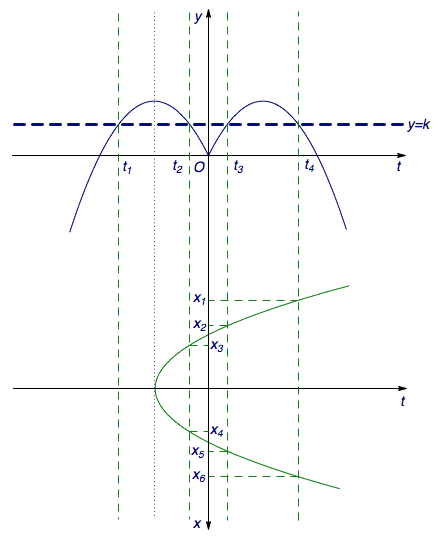
我们无法画出第一个函数的草图，因此需要借助复合函数将其分解为两个较为简单的函数

$$y=-t^2+2|t|,t=x^2-1,$$ 然后组合在一起，如图．

通过两个函数的草图，可以利用函数$y=-t^2+2|t|$的图象由$k$确定对应的$t$的分布．问题的复杂性在于不同的$t$对应的$x$的值的个数可能是不一样的，这需要利用函数$t=x^2-1$的图象来确定．

事实上，当$t>-1$时，每个$t$对应$2$个$x$；当$t=-1$时，每个$t$对应$1$个$x$；当$t<-1$时，每个$t$对应$0$个$x$．

例如，如果直线$y=k$与函数$y=-t^2+2|t|$的图象的交点横坐标落在区间$(-\infty,-1)$上，那么这种交点（如$t_1$）是找不到对应的$x$的；而如果直线$y=k$与函数$y=-t^2+2|t|$的图象的交点横坐标落在区间$(-1,+\infty)$上，那么每个交点（如$t_2$）都可以找到两个$x$的值与之对应（也就是方程的两个不同的根）．

因此不难得到答案，原方程根的个数为

$$\begin{cases}2,&k<0\\4,&k=0\\6,&0<k<1\\3,&k=1\\0,&k>1\end{cases}.$$

---

注    在这道题中，我们并不需要考虑不同的$t$的值所对应的$x$的值是否会发生重复的情况．但在更为复杂的一些试题中，这是非常容易疏忽的地方．