已知函数\(f(x)=ax-{\rm e}^x\),若存在实数\(x\),使得\(f(x)\geqslant 0\),求\(a\)的取值范围.
正确答案是\((-\infty,0)\cup [{\rm e},+\infty)\).
解 分离变量法
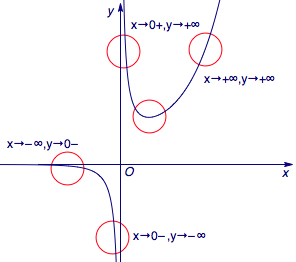
问题即\[\exists x\in \mathcal R,ax-{\rm e}^x\geqslant 0,\]也即\[\left(\exists x>0,a\geqslant \dfrac{{\rm e}^x}{x}\right)\lor \left(\exists x<0,a<\dfrac{{\rm e}^x}{x}\right),\]接下来需要绘制\(g(x)=\dfrac{{\rm e}^x}{x}\)的草图.
注意到函数\(g(x)\)的定义域为\((-\infty,0)\cup (0,+\infty)\),且函数\(g(x)\)的导函数为\[g'(x)=\dfrac{{\rm e}^x}{x^2}\cdot (x-1),\]于是函数在\((-\infty,0)\),\((0,1)\)上单调递减,在\((1,+\infty)\)上单调递增.
于是绘制草图,如图.需要注意的是代表定义域的四个区间端点处的函数值的估计.五个要点任何一点没有注意到都容易引起错误.
进而不难得到\(a\)的取值范围是\((-\infty,0)\cup [{\rm e},+\infty)\).
半分离变量法
问题即\[\exists x\in\mathcal R,ax\geqslant {\rm e}^x,\]于是计算函数\(y={\rm e}^x\)过原点的切线,作图如下:
不难得到\(a\)的取值范围是\((-\infty,0)\cup [{\rm e},+\infty)\).
不分离变量法
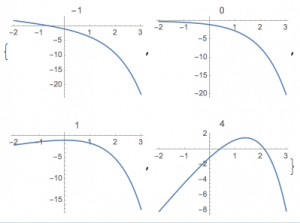
函数\(f(x)\)的导函数\[f'(x)=a-{\rm e}^x,\]于是需要按\(a\)进行讨论.
当\(a<0\)时,\(f(x)\)单调递减.考虑到\(x\to -\infty\)时,\(f(x)\to +\infty\),而当\(x\to +\infty\)时,\(f(x)\to -\infty\).于是符合题意;
当\(a=0\)时,\(f(x)\)单调递减.考虑到\(x\to -\infty\)时,\(f(x)\to 0-\),而当\(x\to +\infty\)时,\(f(x)\to -\infty\).于是不符合题意;
当\(a>0\)时,函数\(f(x)\)有极大值,同时也是最大值,为\(f\left(\ln a\right)=a\left(\ln a-1\right)\),根据题意,最大值不小于\(0\),于是可以解得\(a\geqslant {\rm e}\).
综上,\(a\)的取值范围是\((-\infty,0)\cup [{\rm e},+\infty)\).