在我看来,数学能力由相辅相成的两部分组成:偏感性的直觉、观察能力、创造思维、发散思维;偏理性的验证、运算能力、逻辑思维、聚焦思维.今天再带来一道同时融合代数运算与几何观察的试题.
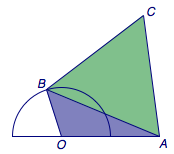
如图,已知半径为\(1\)的半圆\(O\)以及圆外一点\(A\),\(OA=2\).点\(B\)为圆\(O\)上任意一点,以\(AB\)为底向外作正三角形\(ABC\).
(1)求四边形\(OACB\)面积的最大值;
(2)求线段\(OC\)长度的最大值.
解 (1)将四边形划分为两个均以\(AB\)为底的三角形.
为了求四边形\(OACB\)面积的最大值,我们引入变量\(x=\angle AOB\),\(x\in\left[ 0,\pi\right]\).建立四边形\(OACB\)面积与\(x\)的函数关系式\[\begin{split}S(x)&=\dfrac 12\cdot OA\cdot OB\cdot\sin x+\dfrac{\sqrt 3}4\left(OA^2+OB^2-2\cdot OA\cdot OB\cdot\cos x\right)\\&=\sin x-\sqrt 3\cos x+\dfrac {5\sqrt 3}4\\&=2\sin\left(x-\dfrac{\pi}3\right)+\dfrac{5\sqrt 3}4,\end{split}\]于是当\(x=\dfrac{5\pi}6\)时,\(S(x)\)取得最大值\(2+\dfrac{5\sqrt 3}4\).
(2)将\(O\)绕点\(A\)旋转\(\dfrac{\pi}3\)到\(O'\),则三角形\(AOB\)与三角形\(AO'C\)旋转全等,如图.
于是\(OC\)的最大值为\(OO'+O'C=3\),当且仅当\(\angle AOB=\dfrac{2\pi}3\)时取得.
注 上一次是情人节 每日一题[27] 德艺双馨.