向量的数量积运算有明确的几何意义，合理利用几何意义可以有效减少计算．特别是在探索对于与动点相关的数量积的最值问题中的最值点位置时，往往可以起到一矢中的的效果．
2014年高考数学浙江卷（文科）第9题：
设\(\theta\)为两个非零向量\(\overrightarrow{a}\)，\(\overrightarrow{b}\)的夹角，已知对任意实数\(t\)，\(\left|\overrightarrow{b}+t\overrightarrow{a}\right|\)的最小值为\(1\)，则下列说法正确的有______．
① 若\(\theta\)确定，则\(\left|\overrightarrow{a}\right|\)唯一确定；
② 若\(\theta\)确定，则\(\left|\overrightarrow{b}\right|\)唯一确定；
③ 若\(\left|\overrightarrow{a}\right|\)确定，则\(\theta\)唯一确定；
④ 若\(\left|\overrightarrow{b}\right|\)确定，则\(\theta\)唯一确定．
正确答案是 ②．
解 取\(\overrightarrow{OB}=\overrightarrow{b}\)，\(\overrightarrow{BA}=\overrightarrow{a}\)，则\(t\overrightarrow{a}\)在直线\(BA\)上运动，有\(\overrightarrow{b}+t\overrightarrow{a}=\overrightarrow{OA}\)，如图 
已知条件\[\forall t\in\mathcal{R}，\left|\overrightarrow{b}+t\overrightarrow{a}\right|_{\min}=1\]等价于点\(O\)到直线\(BA\)的距离为\(1\)，即\[\left|\overrightarrow{b}\right|\cdot\sin\theta=1.\]由此知只有 ② 正确． ④ 是比较容易错选的结果，事实上可能有两个互补的角同时满足条件．
下面给出一道练习（2013年浙江高考理７，有不影响本质的修改）：
设\(\triangle ABC\)，\(P_0\)是边\(AB\)上一定点，满足\(P_0B=\dfrac 14AB\)，且对于边\(AB\)上任一点\(P\)，恒有\(\overrightarrow{PB}\cdot\overrightarrow{PC}\geqslant \overrightarrow{P_0B}\cdot\overrightarrow{P_0C}\)，则\(\triangle ABC\)的形状为______．
答案 等腰三角形
提示 本题的条件可以翻译为:点\(P\)在边\(AB\)上运动，当\(P=P_0\)时，\(\overrightarrow{PB}\cdot\overrightarrow{PC}\)有最小值． 过点\(C\)作\(CH\perp AB\)于点\(H\)，则\[\overrightarrow{PB}\cdot\overrightarrow{PC}=\overrightarrow{PB}\cdot\overrightarrow{PH},\]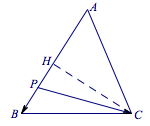 
容易知道当点\(P\)为\(BH\)的中点时，\(\overrightarrow{PB}\cdot\overrightarrow{PH}\)有最小值． 于是知\(P_0B=\dfrac 14AB\)时，\(P_0\)恰为\(BH\)的中点，所以\(AC=BC\)．
更多例题参见 每日一题[227] 向量的几何意义．