与函数不等式相关的问题往往与函数的单调性相关,此时的解析式更像是给出函数性质的一个载体,而与具体的形式关系不大.函数不等式问题解决的关键就在于将函数不等式转化成与自变量相关的不等式,这通常通过探索函数的性质以及对函数不等式进行变形得到.
设\(f(x)\)是定义在\(\mathcal{R}\)上的奇函数,且当\(x\geqslant 0\)时,\(f(x)=x^2\),若对于任意的\(x\in [t,t+2]\),不等式\(f(x+t)\geqslant 2f(x)\)恒成立,则实数\(t\)的取值范围是_____.
正确的答案是\([\sqrt 2,+\infty)\).
我们见过类似的问题,比如:
函数\(g(x)\)是奇函数,且在\(\mathcal{R}\)上单调递减,解不等式\(g(x)+g(x^2)<0\).
此不等式等价于\[g(x)<-g(x^2)=g(-x^2),\]于是函数不等式转化成与自变量相关的不等式\[x>-x^2,\]从而得到结果.
在本题中函数不等式中的负号变成了系数\(2\).
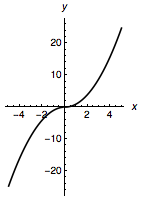
解 根据题意,有\[f(x)=\begin{cases}x^2,&x\geqslant 0,\\-x^2,&x<0.\end{cases}\]
如图,\(f(x)\)具有很好的单调性——在\(\mathcal{R}\)上单调递增.
如果能将系数\(2\)转移到自变量中,则可以和上面的题一样,根据单调性将函数不等式变成普通的不等式.
有了这个方向,不难得到\(2f(x)=f(\sqrt 2x)\),所以\[\forall x\in [t ,t+2],f(x+t)\geqslant f(\sqrt 2 x),\]即\[\forall x\in [t ,t+2],x+t\geqslant \sqrt{2} x,\]从而有\[\left(\sqrt 2-1\right)(t+2)\leqslant t,\]解得\(t\geqslant \sqrt 2\).
下面给一道练习:
设函数\(f(x)=\ln(1+|x|)-\dfrac{1}{1+x^2}\),则使得\(f(x)>f(2x-1)\)成立的\(x\)的取值范围是_____.
答案 \(\left(\dfrac 13,1\right)\).
提示 函数\(f(x)\)是偶函数,且在\([0,+\infty)\)上单调递增(复合函数的单调性).
于是有\[f(x)=f(|x|)>f(2x-1)=f(|2x-1|),\]从而有\[|x|>|2x-1|,\]
这也是一种转化,将自变量都转化到同一个单调区间上来,直接用性质.