每日一题[20] 代数条件的直观化

这是2013年全国新课标I卷理科数学的选择题最后一题（第12题），主要考察变化中的规律探索．同时，本题也是代数条件直观化的一道好题．数形结合思想最强大、最优美的一面就是：对繁杂晦涩的代数算式运用几何直观的方式将蕴含的本质挖掘出来，从而使得问题获得极大简化．

设三角形\(A_nB_nC_n\)的三边长分别为\(a_n,b_n,c_n\)，三角形\(A_nB_nC_n\)的面积为\(S_n\)，\(n=1,2,3,\cdots\)，若\(b_1>c_1\)，\(b_1+c_1=2a_1\)，且满足\[\begin{split}a_{n+1}&=a_n,\\b_{n+1}&=\frac{c_n+a_n}2,\\c_{n+1}&=\frac{b_n+a_n}2,\end{split}\]则（        ）

A．\(\{S_n\}\)为递减数列

B．\(\{S_n\}\)为递增数列

C．\(\{S_{2n-1}\}\)为递增数列，\(\{S_{2n}\}\)为递减数列

D．\(\{S_{2n-1}\}\)为递减数列，\(\{S_{2n}\}\)为递增数列

正确答案是B．

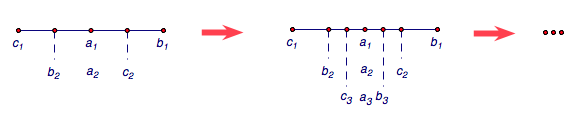
首先，先将条件\(b_1>c_1\)和\(b_1+c_1=2a_1\)直观化，这是容易的，假想数轴上从左到右顺次三个点分别表示\(c_1,a_1,b_1\)，其中\(a_1\)表示的点为中点，如图．

接下来，根据已知条件\(a_n\)表示的点位置保持不变，而\(b_{n+1}\)表示的点为\(c_n\)与\(a_n\)表示的两点的中点，\(c_{n+1}\)表示的点为\(b_n\)与\(a_n\)表示的两点的中点，如图．

这样我们就发现三个关键：①\(b_n\)与\(c_n\)的和为定值；②\(b_n\)与\(c_n\)的距离越来越近；③\(b_n\)与\(c_n\)的大小关系不停的交换．

循此思路，将以上三点选择合适的几何载体表示出来（注意，①给了我们足够的启示：椭圆），如图．

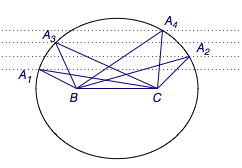
因此\(S_n\)逐步增大，选项B是正确的．