每日一题[19] 解三角形试题的一题两解

平面向量、三角和复数是代数与几何在高中数学中融合最为紧密的部分，在这些部分中一题多解也是最为常见的．今天就给大家带来一道自主招生训练题，一起来感受一下．

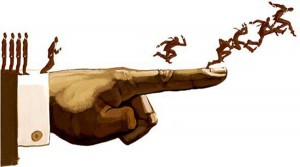如图，$P$为三角形$ABC$内部一点，且满足$\angle BAP=\angle CAP=\angle CBP=\angle ACP$，求证：$BC^2=AC\cdot AB$．

---

法一    三角方法

根据燕尾定理，我们有 $$\angle BPC=A+B,\angle CPA=B+C,\angle APB=C+A.$$

于是，在三角形$BPC$中，由正弦定理有 $$\frac{BC}{\sin\angle BPC}=\frac{PC}{\sin\angle CBP},$$ 在三角形$PAC$中，由正弦定理有 $$\frac{AC}{\sin\angle CPA}=\frac{PC}{\sin\angle CAP},$$ 而根据已知条件有$\angle CBP=\angle CAP$，因此 $$\frac{BC}{\sin\angle BPC}=\frac{AC}{\sin\angle CPA},$$ 即 $$\frac{BC}{\sin(A+B)}=\frac{AC}{\sin(B+C)},$$ 也即 $$\frac{BC}{\sin C}=\frac{AC}{\sin A}.$$ 同时，在三角形$ABC$中，由正弦定理有 $$\frac{AB}{\sin C}=\frac{BC}{\sin A},$$ 两式相比，整理即得 $$BC^2=AC\cdot AB.$$

---

法二    几何方法

不妨设$\angle ABP>\angle CBP$（如果相等，那么$P$为三角形$ABC$的内心，继而$ABC$为正三角形，命题显然成立）．

在边$AC$上取一点$Q$，使得$\angle QBP=\angle PBC$，连接$PQ$．

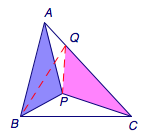
$\because\angle QBP=\angle PAQ$

$\therefore A,B,P,Q$四点共圆

$\therefore\angle PQC=\angle PBA$

又$PC=PA$，$\angle PCQ=\angle PAB$

$\therefore\triangle PCQ\cong\triangle PAB$

$\therefore CQ=AB$

又$\triangle CBQ\sim\triangle CAB$

$\therefore CB^2=CQ\cdot CA$

于是$BC^2=AB\cdot CA$，命题得证．

---

这次还给大家带来了两道练习题哦，可以从三角和几何两个不同的角度思考．

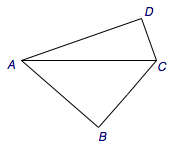
第一题    如图，$\angle ABC=\angle ADC=90^\circ$，$\angle BAD=60^\circ$，$BC=2CD=2$，求$AC$．

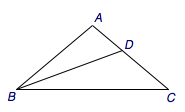
第二题    如图，在等腰三角形$ABC$中，已知$A=100^\circ$，$B$的平分线交$AC$于$D$，求证：$AD+DB=BC$．