每日一题[234] 分离变量

2014年高考天津卷理科数学第14题：

已知函数\(f(x)=\left|x^2+3x\right|\)，\(x\in\mathcal R\)．若方程\(f(x)-a\left|x-1\right|=0\)恰有\(4\)个互异的实数根，则实数\(a\)的取值范围是_______．

正确答案是\((0,1)\cup (9,+\infty)\)．

解    换元，令\(t=x-1\)，则问题转化为方程\[\left|(t+1)^2+3(t+1)\right|-a|t|=0\]有\(4\)个互异的实数根，也即方程\[a=\left|t+\dfrac 4t+5\right|\]有\(4\)个互异的实数根．

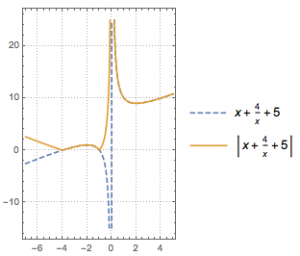
如图，作出函数\(y=\left|x+\dfrac 4x+5\right|\)的图象，其极大值点为\((-2,1)\)，极小值点为\((2,9)\)，于是可得实数\(a\)的取值范围是\((0,1)\cup (9,+\infty)\)．

注    处理含参数的函数\(f(x,a)=0\)零点问题一般有三种处理方式：

1、不分离

直接根据参数\(a\)讨论函数图象，并研究其零点；

2、半分离

将方程转化为\(g(x)=kx+b\)的形式，然后利用直线与曲线的位置关系研究；

3、全分离

将方程转化为\(g(x)=h(a)\)的形式，然后研究方程\(t=g(x)\)的零点得到\(t\)的取值范围后将该范围转化为\(a\)的取值范围．

下面给出一道练习题．

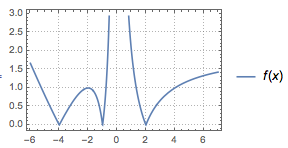
（2014年·天津·文14）已知函数\(f(x)=\begin{cases}\left|x^2+5x+4\right|,&x\leqslant 0\\2|x-2|,&x>0.\end{cases}\)若函数\(y=f(x)-a|x|\)恰有\(4\)个零点，则实数\(a\)的取值范围是_______．

答案    \((1,2)\)

提示    如图．