利用三角形五心的向量表达（可以参考2015年1月27日每日一题）：
重心\(G\)满足
\[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0,\]
外心\(O\)满足
\[\sin 2A\overrightarrow{OA}+\sin 2B\overrightarrow{OB}+\sin 2C\overrightarrow{OC}=\overrightarrow 0,\]
内心\(I\)满足
\[\begin{split}a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow 0,\\\sin A\overrightarrow{IA}+\sin B\overrightarrow{IB}+\sin C\overrightarrow{IC}=\overrightarrow 0\end{split}\]
垂心\(H\)满足
\[\tan A\overrightarrow{HA}+\tan B\overrightarrow{HB}+\tan C\overrightarrow{HC}=\overrightarrow 0,\]
旁心\(I_A\)满足
\[-\sin A\overrightarrow{I_AA}+\sin B\overrightarrow{I_AB}+\sin C\overrightarrow{I_AC}=\overrightarrow 0.\]
我们可以有效地通过代数计算来证明很多和三角形的五心相关的几何命题，比如：
在三角形\(ABC\)中，角\(A\)、\(B\)、\(C\)所对的边分别为\(a\)、\(b\)、\(c\)，且\(2a=b+c\)．\(O\)、\(I\)分别为\(\triangle ABC\)的外心和内心，求证：\(OI\perp AI\)．
利用之前2015年1月27日每日一题中的结论，我们有
\[\begin{split}\overrightarrow{AI}\cdot\overrightarrow{OI}&=\overrightarrow{AI}\cdot\left(\overrightarrow{AI}-\overrightarrow{AO}\right)\\&=\left(\dfrac{b}{a+b+c}\overrightarrow{AB}+\dfrac{c}{a+b+c}\overrightarrow{AC}\right)\cdot\left(\dfrac{b}{a+b+c}\overrightarrow{AB}+\dfrac{c}{a+b+c}\overrightarrow{AC}\right)\\&\qquad -\left(\dfrac{b}{a+b+c}\overrightarrow{AB}+\dfrac{c}{a+b+c}\overrightarrow{AC}\right)\cdot\overrightarrow{AO}\\&=\dfrac{1}{(a+b+c)^2}\left(b^2\overrightarrow{AB}\cdot\overrightarrow{AB}+2bc\overrightarrow{AB}\cdot\overrightarrow{AC}+c^2\overrightarrow{AC}\cdot\overrightarrow{AC}\right)\\&\qquad -\dfrac{1}{a+b+c}\left(b\overrightarrow{AB}\cdot\overrightarrow{AO}+c\overrightarrow{AC}\cdot\overrightarrow{AO}\right)\\&=\dfrac{2b^2c^2+bc(b^2+c^2-a^2)}{(a+b+c)^2}-\dfrac{\dfrac 12bc^2+\dfrac 12b^2c}{a+b+c}\\&=\dfrac{bc(b+c-2a)}{2(a+b+c)}\\&=0.\end{split}\]
因此原命题得证．
对这种方法感兴趣的同学还可以尝试一下下面这两道习题：
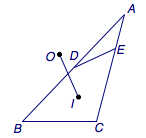
1、在三角形\(ABC\)中，角\(A\)、\(B\)、\(C\)所对的边分别为\(a\)、\(b\)、\(c\)，且\(a<b<c\)．\(D\)、\(E\)分别在边\(AB\)、\(AC\)上，且\(BD=CE=a\)，\(O\)、\(I\)分别为三角形\(ABC\)的外心和内心，求证：\(OI\perp DE\)．
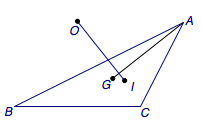
2、如图，\(O\)、\(G\)、\(I\)分别为三角形\(ABC\)的外心、重心、内心，且\(AG\perp OI\)，求证：\[\dfrac 1b+\dfrac 1c=\dfrac 2a.\]
