2014年高考安徽卷理科数学第10题(选择压轴题):
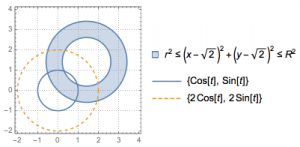
在平面直角坐标系\(xOy\)中,已知向量\(\overrightarrow a,\overrightarrow b\),\(\left|\overrightarrow a\right|=\left|\overrightarrow b\right|=1\),\(\overrightarrow a\cdot \overrightarrow b=0\),点\(Q\)满足\(\overrightarrow{OQ}=\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)\),曲线\(C=\left\{P\left|\overrightarrow{OP}=\cos\theta\overrightarrow a+\sin\theta\overrightarrow b,0\leqslant \theta<2\pi\right.\right\}\),区域\(\Omega=\left\{P\left|0<r\leqslant \left|\overrightarrow{PQ}\right|\leqslant R,r<R\right.\right\}\).若\(C\cap \Omega\)为两段分离的曲线,则( )
A.\(1<r<R<3\)
B.\(1<r<3\leqslant R\)
C.\(r\leqslant 1<R<3\)
D.\(1<r<3<R\)
正确答案为 A.
解 注意到\[\begin{split}\overrightarrow{OQ}\cdot\overrightarrow{OQ}&=\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)\cdot\sqrt 2\left(\overrightarrow a+\overrightarrow b\right)\\&=2\left|\overrightarrow a\right|^2+2\left|\overrightarrow b\right|^2\\&=4,\end{split}\]于是\(Q\)在以\(O\)为圆心,\(2\)为半径的圆上.
另一方面,类似可得\[\begin{split}\overrightarrow{OP}\cdot\overrightarrow{OP}&=\left(\cos\theta\overrightarrow a+\sin\theta\overrightarrow b\right)\cdot \left(\cos\theta\overrightarrow a+\sin\theta\overrightarrow b\right)\\&=\cos^2\theta\left|\overrightarrow a\right|^2+\sin^2\theta\left|\overrightarrow b\right|^2\\&=1,\end{split}\]于是曲线\(C\)是以\(O\)为圆心,\(1\)为半径的圆.
据此,我们可以画出示意图,题意即圆心在虚圆上的圆环(“和氏璧”)截实圆为两段分离的弧,于是\(r>1\land R<3\),选项 A 符合题意.
注 插图为秘鲁的Moray,一个发挥到极致的印加梯田,传说的圆环套圆环.