2014年高考数学湖北卷第10题(选择压轴题):
已知函数\(f(x)\)是定义在\(\mathcal R\)上的奇函数,当\(x\geqslant 0\)时,\(f(x)=\dfrac{1}{2}\left(\left|x-a^2\right|+\left|x-2a^2\right|-3a^2\right)\).若\(\forall x\in \mathcal R,f(x-1)\leqslant f(x)\),则实数\(a\)的取值范围是( )
A.\(\left[-\dfrac 16,\dfrac 16\right]\)
B.\(\left[-\dfrac{\sqrt 6}6,\dfrac{\sqrt 6}6\right]\)
C.\(\left[-\dfrac 13,\dfrac 13\right]\)
D.\(\left[-\dfrac{\sqrt 3}3,\dfrac{\sqrt 3}3\right]\)
正确答案是B.
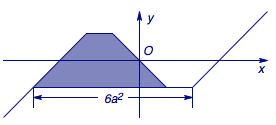
用分界点\(x=a^2\)和\(x=2a^2\)讨论,不难画出函数的草图.
题目中的条件\(\forall x\in\mathcal R,f(x-1)\leqslant f(x)\)的意思就是设法通过平移一个单位,把函数图象中的“山”(阴影部分)藏在右边的图象下方(包括边界).
事实上,“山”的宽度为\(6a^2\),于是由不等式\[6a^2\leqslant 1\]解得实数\(a\)的取值范围是\(\left[-\dfrac{\sqrt 6}6,\dfrac{\sqrt 6}6\right]\).
下面给出一道练习题.
设函数\(f(x)\)的定义域为\(D\),若存在非零实数\(l\)使得对于任意\(x\in M\)(\(M\subseteq D\)),有\(x+l\in D\),且\(f(x+l)\geqslant f(x)\),则称\(f(x)\)为\(M\)上的\(l\)高调函数.
(1)如果定义域为\(\left[-1,+\infty\right)\)的函数\(f(x)=x^2\)为\(\left[-1,+\infty\right)\)上的\(m\)高调函数,那么实数\(m\)的取值范围是_______.
(2)如果定义域为\(\mathcal R\)的函数\(f(x)\)是奇函数,当\(x\geqslant 0\)时,\(f(x)=\left|x-a^2\right|-a^2\),且\(f(x)\)为\(\mathcal R\)上的\(4\)高调函数,那么实数\(a\)的取值范围是_______.
(3)现给出下列命题:
① 函数\(f(x)=\left(\dfrac 12\right)^x\)为\(\mathcal R\)上的\(1\)高调函数;
② 函数\(f(x)=\sin 2x\)为\(R\)上的\(\pi \)高调函数;
③ 如果定义域为\(\left[-1,+\infty\right)\)的函数\(f(x)=x^2\)为\(\left[-1,+\infty\right)\)上的\(m\)高调函数,那么实数\(m\)的取值范围是\(\left[2,+\infty\right)\).
其中正确的命题是_______.
答案 (1)\(m\geqslant 2\);(2)\(\left[-1,1\right]\);(3)②③.


妙极了!