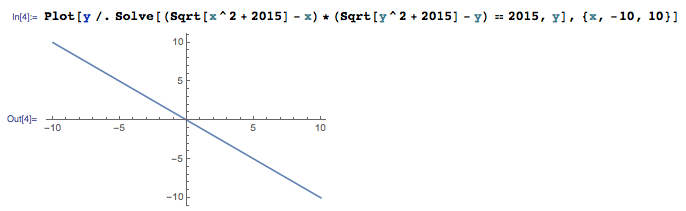已知实数\(x,y\)满足\[\left(\sqrt{x^2+2015}-y\right)\cdot\left(\sqrt{y^2+2015}-x\right)=2015,\]求\(x+y\)的值.
正确答案是\(0\).
此题应是由2009年的一道初中竞赛题改编而来,原题为
已知实数\(x,y\)满足\[\left(\sqrt{x^2+2009}-x\right)\cdot\left(\sqrt{y^2+2009}-y\right)=2009,\]求\(x+y\)的值.
略解如下:
根据已知,有\[\sqrt{x^2+2009}-x=\dfrac{2009}{\sqrt{y^2+2009}-y}=\sqrt{y^2+2009}+y,\]于是有\[x+y=\dfrac{x^2-y^2}{\sqrt{x^2+2009}+\sqrt{y^2+2009}},\]于是\(x+y=0\),或\[ x-y=\sqrt{x^2+2009}+\sqrt{y^2+2009}.\]考虑到\(x,y\)的对称性,若\(x+y\neq 0\)则必然亦有\[y-x=\sqrt{y^2+2009}+\sqrt{x^2+2009},\]两式相加得\[0=2\sqrt{x^2+2009}+2\sqrt{y^2+2009},\]矛盾.
经验证,\(x+y=0\)时原式成立,因此\(x+y\)的值为\(0\).
我们用相同的方式处理本题.
根据已知,有\[\sqrt{x^2+2015}-y=\dfrac{2015\left(\sqrt{y^2+2015}+x\right)}{y^2-x^2+2015},\]整理得\[\left(x^2-y^2\right)\left(y-\sqrt{x^2+2015}\right)+\dfrac{2015\left(x^2-y^2\right)}{\sqrt{x^2+2015}+\sqrt{y^2+2015}}-2015(x+y)=0,\]于是有\(x+y=0\),或\[\left(x-y\right)\left(y-\sqrt{x^2+2015}\right)+\dfrac{2015(x-y)}{\sqrt{x^2+2015}+\sqrt{y^2+2015}}-2015=0,\]类似的,考虑到\(x,y\)的对称性,若\(x+y\neq 0\)则必然亦有\[\left(y-x\right)\left(x-\sqrt{y^2+2015}\right)+\dfrac{2015(y-x)}{\sqrt{y^2+2015}+\sqrt{x^2+2015}}-2015=0,\]两式相加有\[(x-y)\left(y-x+\sqrt{y^2+2015}-\sqrt{x^2+2015}\right)-4030=0,\]即\[-(x-y)^2\left(1+\dfrac{x+y}{\sqrt{x^2+2015}+\sqrt{y^2+2015}}\right)=4030,\]事实上,有\[x+y\geqslant -\sqrt{x^2+2015}-\sqrt{y^2+2015},\]因此\[-(x-y)^2\left(1+\dfrac{x+y}{\sqrt{x^2+2015}+\sqrt{y^2+2015}}\right)\leqslant 0,\]矛盾.
经验证,\(x+y=0\)时原式成立,因此\(x+y\)的值为\(0\).
另法 (由郭岩提供)
先证明\[\sqrt{x^2+2015}-y>0\land \sqrt{y^2+2015}-x>0,\]具体过程从略.
再证明\(x+y=0\).用反证法,若不然,当\(x+y>0\)时,不妨设\(x\geqslant y\),则有\[x>0,x\geqslant y>-x,\]于是\[y^2\leqslant x^2,\]有\[\sqrt{y^2+2015}-x\leqslant \sqrt{x^2+2015}-x,\]而另一方面,\[\sqrt{x^2+2015}-y<\sqrt{x^2+2015}+x,\]于是\[LHS\leqslant \left(\sqrt{x^2+2015}+x\right)\cdot\left(\sqrt{x^2+2015}-x\right)=2015,\]矛盾.
当\(x+y<0\)时,同理可证.
经验证,\(x+y=0\)时原式成立,因此\(x+y\)的值为\(0\).