在平面直角坐标系\(xOy\)中,设\(A,B,C\)是平面上不同的三点,并且都在圆\(x^2+y^2=1\)上,若存在实数\(\lambda,\mu\)使得\(\overrightarrow{OC}=\lambda \overrightarrow{OA}+\mu\overrightarrow{OB}\),则\(\left(\lambda -3\right)^2+\mu^2\)的取值范围是_______.
解 设\(\overrightarrow{OA}\cdot\overrightarrow{OB}=m\),则考虑到\(A,B,C\)是不同的三点,且均在单位圆上,于是\(m\)的取值范围为\((-1,1)\).
由已知有\[\overrightarrow{OC}\cdot\overrightarrow{OC}=\left(\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}\right)\cdot\left(\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}\right),\]从而\[1=\lambda^2+\mu^2+2m\lambda\mu,\]进而可得当\(\lambda\mu>0\)时,有\[1>\lambda^2+\mu^2-2\lambda\mu,\]从而\[-1<\lambda-\mu<1.\]而类似的,当\(\lambda\mu<0\)时,有\[1>\lambda^2+\mu^2+2\lambda\mu,\]从而\[-1<\lambda+\mu<1.\]
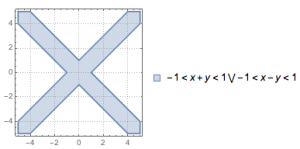
于是将\(y=\left(\lambda-3\right)^2+\mu^2\)视为可行域内的点\(\left(\lambda,\mu\right)\)到点\((3,0)\)的距离之平方,可得该值在\((2,+\infty)\)内(注意:上图中的阴影区域并不是可行域).
当\(\left(\lambda,\mu\right)\to\left(2,-1\right)\)时,\(y\to 2\);
当\(\lambda\to +\infty\)而\(\mu=1-\lambda\)时,\(y\to +\infty\).
因此,所求的取值范围是\((2,+\infty)\).
另法 (由郭岩提供)设\(\overrightarrow{OC}\cdot\overrightarrow{OA}=t\),\(t\in (-1,1)\),则由\[\overrightarrow{OC}-\lambda\overrightarrow{OA}=\mu\overrightarrow{OB}\]得\[\lambda^2-2t\lambda +1=\mu^2,\]于是\[\begin{split}\left(\lambda-3\right)^2+\mu^2&=\lambda^2-6\lambda+9+\lambda^2-2t\lambda+1\\&=10+2\left(\lambda-\dfrac{t+3}{2}\right)^2-\dfrac 12\left(t+3\right)^2\\&\geqslant 10-\dfrac 12\left(t+3\right)^2\\&>2,\end{split}\]以下略.
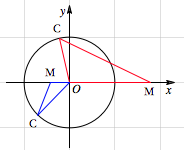
另法 (由梅云提供)由题意可设\(\overrightarrow{OM}=\lambda\overrightarrow{OA}\),\(\overrightarrow{MC}=\mu\overrightarrow{OB}\),则\(\lambda\),\(\mu\),\(1\)构成三角形\(OMC\)的三边(否则\(A,B,C\)中至少有两个点重合),如图:
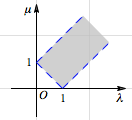
于是\(\lambda\)与\(\mu\)满足\[\begin{cases}\lambda>0,\\\mu>0,\\\lambda+\mu>1,\\\lambda+1>\mu,\\\mu+1>\lambda\end{cases}\]
得到的可行域所在的区域如下:
以下略.
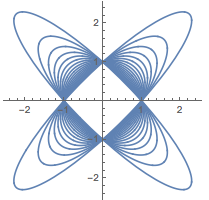
注 事实上,当\(m\)取不同的值时,方程\[1=\lambda^2+\mu^2+2m\lambda\mu\]表示不同的椭圆,它们都经过\((0,\pm 1)\)及\((\pm 1,0)\)四点,如图所示.
当\(m\)取遍\((-1,1)\)内的所有实数时,点\(\left(\lambda,\mu\right)\)形成的可行域如图(此图中\(\lambda\)从\(-0.99\)取到\(0.99\),间隔为\(0.02\)).


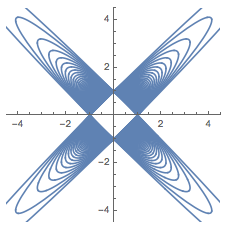
梅云那个方法里面构成AMC的三边和mu是不是都应该加绝对值啊,从而最后的图形在四个象限都有取值。
原题是有正实数条件的,我后来给撤掉了.