2014年全国高中数学联赛山东省预赛第12题：
已知函数\(f_1(x)=f(x)=x(x-1)\)，\(f_n(x)=f\left(f_{n-1}(x)\right)\)，其中\(n\geqslant 2\)．求证：
（1）当\(x>2\)时，\(f_n(x)\)没有零点；
（2）当\(1\leqslant x\leqslant 2\)时，\(f_n(x)\)至少有\(n\)个零点．
（1）证明 由于当\(x>2\)时，\(f(x)>2\)，因此可以递推至\(f_n(x)>2\)．
（2）证明 用数学归纳法证明．
当\(n=1\)时，\(f(x)=x(x-1)\)在\([1,2]\)上有零点为\(1\)；
假设命题对\(n\)成立，即\(f_n(x)\)至少有\(n\)个零点，从小到大设为\(x_i\)，\(i=1,2,\cdots,n\)．
考虑函数\(f_{n+1}(x)=f\left(f_{n}(x)\right)\)的零点，即\[f_n(x)=0\lor f_n(x)=1,\]第一个方程根据归纳假设有根\(x=x_i\)，\(i=1,2,\cdots,n\)．而另一方面，根据\[\begin{cases}f_n\left(x_n\right)-1=-1<0,\\f_n(2)-1=1>0,\end{cases}\]因此由零点的存在性定理可得方程\(f_n(x)=1\)至少有一个在\(\left(x_n,2\right)\)上的根．
于是函数\(f_{n+1}(x)\)至少有\(n+1\)个零点，命题对\(n+1\)也成立．
综上，命题得证．
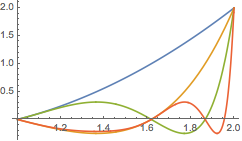
注 如图，可以看出每次迭代会在最右侧生成一个新的零点．
