每日一题[189]代数式的最值

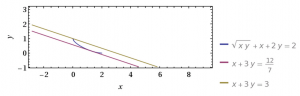
已知$x+2y+\sqrt{xy}=2$，求$x+3y$的取值范围．

首先，$x\geqslant 0$，$y\geqslant 0$．否则 $$x+2y+\sqrt{xy}\leqslant -2\sqrt{2xy}+\sqrt{xy}\leqslant 0,$$ 与已知条件矛盾．

法一    待定参数

将参数引入均值不等式，有 $$\sqrt{xy}\leqslant \dfrac 12\left(\lambda x+\dfrac{y}{\lambda}\right),\lambda>0$$ 于是 $$\begin{split}2&=x+2y+\sqrt{xy}\\&=x+2y+\dfrac{\lambda}{2}\cdot x+\dfrac{1}{2\lambda}\cdot y\\&=\left(1+\dfrac{\lambda}{2}\right)x+\left(2+\dfrac{1}{2\lambda}\right)y,\end{split}$$ 令$x$、$y$的系数比为$1:3$得待定系数$\lambda=\dfrac 13$，因此可得 $$x+3y\geqslant \dfrac{12}{7},$$ 等号当$x=9y=\dfrac 97$时取得．

也可以这样描述，设 $$\begin{split}\lambda (x+3y)-2&=\lambda x+3\lambda y-x-2y-\sqrt{xy}\\&=\left(\lambda -1\right)x+\left(3\lambda -2\right)y-\sqrt{xy}\\&\geqslant 2\sqrt{\left(\lambda -1\right)\left(3\lambda -2\right)}\cdot \sqrt{xy}-\sqrt{xy},\end{split}$$ 令 $$2\sqrt{\left(\lambda -1\right)\left(3\lambda -2\right)}=1,$$ 得$\lambda=\dfrac 76$，于是可得 $$x+3y\geqslant \dfrac{12}{7},$$ 等号当$x=9y=\dfrac 97$时取得．

另一方面，有 $$x+3y\leqslant \dfrac 32x+3y+\dfrac 32\sqrt{xy}=3,$$ 等号当$x=0\land y=1$时取得．

因此所求代数式的取值范围为$\left[\dfrac{12}7,3\right]$．

法二    三角换元

设$a=\sqrt x$，$b=\sqrt y$，则原问题转化为已知$a^2+2b^2+ab=2$，求$a^2+3b^2$的取值范围．

再令$a=r\cos\theta$，$b=\dfrac{1}{\sqrt 3}\cdot r\sin\theta$，$\theta\in\left[0,\dfrac{\pi}{2}\right]$，$r>0$，则所求代数式即$r^2$，而 $$r^2\cos^2\theta+\dfrac 23r^2\sin^2\theta+\dfrac 1{\sqrt 3}r^2\sin\theta\cos\theta=2,$$ 于是 $$\begin{split}\dfrac 2{r^2}&=\cos^2\theta+\dfrac 23\sin^2\theta+\dfrac{1}{\sqrt 3}\sin\theta\cos\theta\\&=\dfrac 56+\dfrac 13\sin\left(2\theta+\dfrac{\pi}{6}\right),\end{split}$$ 而 $$\dfrac{\pi}{6}\leqslant 2\theta+\dfrac{\pi}{6}\leqslant \dfrac{7\pi}{6},$$ 于是可得 $$\dfrac{12}{7}\leqslant r^2\leqslant 3,$$ 所求取值范围为$\left[\dfrac{12}7,3\right]$．