每日一题[188] 代数式的最值

2015年清华大学自主招生试题：

已知$2x+y=1$，求$x+\sqrt{x^2+y^2}$的最值．

---

正确答案是最小值为$\dfrac 45$，不存在最大值．

法一    判别式

令$m=x+\sqrt{x^2+y^2}$，则

$$x=\dfrac{m^2-y^2}{2m},$$ 因此 $$2\cdot\dfrac{m^2-y^2}{2m}+y=1,$$ 整理得 $$y^2-my+m-m^2=0,$$ 从而判别式 $$\Delta=m^2-4(m-m^2)\geqslant 0,$$ 解得 $$m\geqslant \dfrac 45.$$

其中用到了$m=x+\sqrt{x^2+y^2}\geqslant \sqrt{x^2+y^2}-\sqrt{x^2}\geqslant 0$．

---

法二    三角换元

设$x=r\cos\theta$，$y=r\sin\theta$，则条件转化为

$$2r\cos\theta+r\sin\theta=1,$$ 所求代数式转化为 $$r\cos\theta+r,$$ 于是问题转化为求代数式 $$\dfrac{\cos\theta+1}{2\cos\theta+\sin\theta}$$ 的最值．

记该代数式为$m$，则

$$\cos\theta+1=2m\cos\theta+m\sin\theta,$$ 整理得 $$\sqrt{m^2+(2m-1)^2}\sin\left(\theta+\varphi\right)=1,$$ 于是 $$m^2+(2m-1)^2\geqslant 1,$$ 解得 $$m\geqslant \dfrac 45.$$

容易检验得$\dfrac 45$可以去到，为最小值，而不存在最大值．

---

法三    数形结合

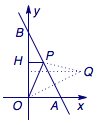
情形一    如图，当$x\geqslant 0$时，设$P$为直线$2x+y=1$上的一点，则

$$x+\sqrt{x^2+y^2}=PO+PH,$$ 根据“将军饮马”问题，该值有最小值，为$O$关于直线$2x+y=1$的对称点$Q\left(\dfrac 45,\dfrac 25\right)$到$y$轴的距离$\dfrac 45$．

情形二    如图，当$x<0$时，设$P$为直线$2x+y=1$上的一点，则

$$x+\sqrt{x^2+y^2}=PO-PH,$$ 而 $$PO>OH=OB+2PH>1+PH,$$ 于是 $$PO-PH>1.$$

综合以上，所求代数式最小值为$\dfrac 45$，不存在最大值．