每日一题[181]定比点差法

2011年高考浙江卷理科数学第16题：

设$F_1$、$F_2$分别为椭圆$\dfrac{x^2}3+y^2=1$的左、右焦点，点$A$、$B$在椭圆上，且$\overrightarrow{F_1A}=5\overrightarrow{F_2B}$，则点$A$的坐标是_______．

正确答案是$(0,1)\lor (0,-1)$．

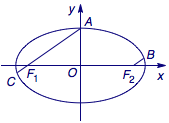
如图，延长$AF_1$交椭圆于$C$，则$\overrightarrow{AF_1}=5\overrightarrow{F_1C}$，设$A(x_1,y_1)$、$C(x_2,y_2)$，则根据定比分点坐标公式有$F_1$的坐标 $$\left(\dfrac{x_1+5x_2}{6},\dfrac{y_1+5y_2}{6}\right)=(-\sqrt 2,0),$$ 从而 $$x_1+5x_2=-6\sqrt 2,y_1+5y_2=0.$$

另一方面，由 $$\dfrac{x_1^2}{3}+y_1^2=1,\dfrac{25x_2^2}{3}+25y_2^2=25$$ 相减可得 $$\dfrac{(x_1+5x_2)(x_1-5x_2)}{3}+(y_1+5y_2)(y_1-5y_2)=-24,$$ 从而可得 $$x_1-5x_2=6\sqrt 2.$$

因此以上两式相加，可得$x_1=0$，进而可得$A=(0,\pm 1)$．

注    （定比分点坐标公式）设$A(x_1,y_1)$、$B(x_2,y_2)$，若$\overrightarrow{AP}=\lambda\overrightarrow{PB}$，$\lambda\neq -1$，则$P$点的坐标为 $$\left(\dfrac{x_1+\lambda x_2}{1+\lambda},\dfrac{y_1+\lambda y_2}{1+\lambda}\right).$$