每日一题[166] 以点构图

2015年高考四川卷理科数学第10题、文科数学第10题（选择压轴题）：

设直线$l$与抛物线$y^2=4x$相交于$A$、$B$两点，与圆$(x-5)^2+y^2=r^2$（$r>0$）相切于点$M$，且$M$为线段$AB$的中点．若这样的直线$l$恰有$4$条，则$r$的取值范围是（        ）

A．$(1,3)$

B．$(1,4)$

C．$(2,3)$

D．$(2,4)$

---

正确答案是D．

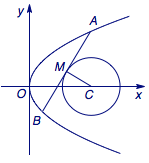
解    如图，记圆心为$C(5,0)$，设$A\left(4a^2,4a\right)$，$B\left(4b^2,4b\right)$．

显然无论$r$为何值，都存在$a+b=0$的两个平凡解（垂直于$Ox$轴的两条切线），因此只需要考虑$a+b\neq 0$的情形．

由于$M\left(2\left(a^2+b^2\right),2(a+b)\right)$，于是根据$AB$与圆$C$相切于$M$，可得

$$\dfrac{2(a+b)-0}{2\left(a^2+b^2\right)-5}\cdot\dfrac{4a-4b}{4a^2-4b^2}=-1,$$ 即 $$a^2+b^2=\frac 32.$$ 于是 $$\begin{split}r^2&=CM^2\\&=\left[2\left(a^2+b^2\right)-5\right]^2+\left[2(a+b)-0\right]^2\\&=4+4(a+b)^2,\end{split}$$ 由 $$0<(a+b)^2<2\left(a^2+b^2\right)=3,$$ 得 $$4<r^2<16,$$ 于是所求$r$的取值范围是$(2,4)$．

---

注一    解析几何习题中，有时利用点的坐标直接表达已知条件要比设直线方程表达交点坐标后再利用交点坐标表达条件要简单有效得多．

注二    有关$r$的取值范围的充分性的考虑，可以借助规划进行．