2015年高考陕西卷理科数学第21题（压轴题）：
设\(f_n(x)\)是等比数列\(1,x,x^2,\cdots,x^n\)的各项和，其中\(x>0\)，\(n\in\mathcal N\)，\(n\geqslant 2\)．
（1）证明： 函数\(F_n(x)=f_n(x)-2\)在\(\left(\dfrac 12,1\right)\)内有且仅有一个零点（记为\(x_n\)），且\(x_n=\dfrac 12+\dfrac 12x_n^{n+1}\)；
（2）设有一个与上述等比数列的首项、末项、项数分别相同的等差数列，其各项和为\(g_n(x)\)，比较\(f_n(x)\)和\(g_n(x)\)的大小，并加以证明．
（1）证明 根据已知，有\[F_n(x)=x+x^2+\cdots+x^n-1,\]于是\[F_n\left(\frac 12\right)=\frac 12+\frac{1}{2^2}+\cdots+\frac{1}{2^n}-1=-\frac{1}{2^n}<0,\]而\[F_n(1)=n-1>0.\]
另一方面，考虑到在\(\left(\dfrac 12,1\right)\)上\[F_n'(x)=1+2x+\cdots+nx^{n-1}>0,\]因此函数\(F_n(x)\)在\(\left(\dfrac 12,1\right)\)上单调递增．
综合以上，函数\(F_n(x)\)在\(\left(\dfrac 12,1\right)\)内有且仅有一个零点．
由\[x_n+x_n^2+\cdots+x_n^n-1=0\]可得\[\dfrac{x_n-x_n^{n+1}}{1-x_n}-1=0,\]整理即得\[x_n=\dfrac 12+\dfrac 12x_n^{n+1}.\]
（2）解与证明 当\(x=1\)时\(f_n(x)=g_n(x)\)；当\(x\neq 1\)时\(f_n(x)<g_n(x)\)，证明如下．
根据题意描述，\(n\geqslant 3\)．
当\(x\geqslant 1\)时，考虑\[h_n(x)=f_n(x)-g_n(x)=1+x+x^2+\cdots+x^n-\frac{n+1}{2}\left(1+x^n\right)\]的导数\[\begin{split}h_n'(x)&=1+2x+\cdots+nx^{n-1}-\frac{n(n+1)}{2}\cdot x^{n-1}\\&=x^{n-1}\left[1\cdot\left(\frac 1x\right)^{n-1}+2\cdot \left(\frac 1x\right)^{n-2}+\cdots+n-\frac{n(n+1)}{2}\right],\end{split}\]于是函数\(h_n(x)\)在\((0,1)\)上单调递增．在\((1,+\infty)\)上单调递减．考虑到\(h_n(1)=0\)，于是结论得证．
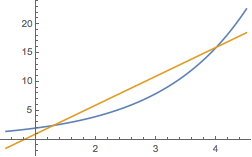
注一 （2）的几何意义为指数函数图象的割线恒在指数函数图象的上方．
因此也可以将\(x\)视为常数，证明当\(x\neq 1\)时\[x^k<1+k\cdot\frac{x^n-1}{n}\]对\(k=0,1,2,\cdots,n\)成立即可．
注二 （2）的本质与2012年高考重庆理科数学第20题（压轴题）的第（2）小题一致，试题如下：
设数列\(\left\{a_n\right\}\)的前\(n\)项和\(S_n\)满足\(S_{n+1}=a_2S_n+a_1\)，其中\(a_2\neq 0\)．
（1）求证：\(\left\{a_n\right\}\)是首项为\(1\)的等比数列；
（2）若\(a_2>-1\)，求证：\(S_n\leqslant \dfrac n2\left(a_1+a_n\right)\)并给出等号成立的充要条件．