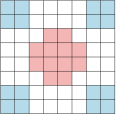
已知集合 $A=\{1,2,3,4,5,6,7,8\}$,$ M=\left\{\left(x_i, y_i\right) \mid x_i \in A, y_i \in A\right\}$,从 $M$ 中选出 $n$ 构成一列:\[\left(x_1, y_1\right), \cdots,\left(x_n, y_n\right).\]相邻两项 $\left(x_i, y_i\right),\left(x_{i+1}, y_{i+1}\right)$ 满足:\[\big( \left|x_{i+1}-x_i\right|,\left|y_{i+1}-y_i\right|\big)=(3,4),~\text{或}~(4,3),\]称为 $k$ 列.
1、若 $k$ 列的第一项为 $(3,3)$,求第二项;
2、若 $\tau$ 为 $k$ 列,且满足 $i$ 为奇数时,$x_i \in\{1,2,7,8\} $;$i$ 为偶数时,$x_i \in\{3,4,5,6\} ;$ 判断:$(3,2)$ 与 $(4,4)$ 能否同时在 $\tau$ 中,并说明;
3、证明:不存在包含 $M$ 中所有元素的 $k$ 列.
解析
1、根据题意,有\[(x_{i+1},y_{i+1})=(x_i,y_i)+(p,q),\]其中\[(p,q)\in\{(3,4),(3,-4),(-3,4),(-3,-4),(4,3),(4,-3),(-4,3),(-4,-3)\},\]而 $x_1=y_1=3$,于是 $p,q\notin\{-3,-4\}$,第二项为 $(6,7)$ 或 $(7,6)$
2、考虑项 $(x_i,y_i)$ 的坐标之和 $x_i+y_i$,引入\[p_i=\begin{cases} 1,&x_i+y_i\equiv 1\pmod 2,\\ 0,&x_i+y_i\equiv 0\pmod 2.\end{cases}\]设 $(3,2),(4,4)$ 分别为 $\tau$ 中的第 $s,t$ 项,则 $p_s=1$ 且 $p_t=0$,而\[3,4\in\{3,4,5,6\}\implies s,t\text{为偶数}\implies p_s=p_t,\]矛盾,因此 $(3,2),(4,4)$ 不能同时在 $\tau$ 中.
如图,根据题设,$k$ 列对应的格子颜色相间,进而位于第 $3,4,5,6$ 列的格子应该同色,矛盾.
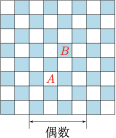
3、记第 $1,2,7,8$ 列为区域 $M$,第 $3,4,5,6$ 列为区域 $N$,由于不存在 $M\to M$ 的情况,因此 $k$ 列的移动路线形如\[ \underbrace{M\to N\to M\to N}_{t~\text{对}}\to \cdots \to \underbrace{N\to M\to N\to M\to \cdots N\to M}_{(32-t)~\text{对}},\]其中 $0\leqslant t\leqslant 32$,$t\in\mathbb N$.注意到区域 $M,N$ 中的两种颜色的格子均为 $16$ 个,因此 $t=16$. 同理,记第 $1,2,7,8$ 行为区域 $P$,第 $3,4,5,6$ 行为区域 $Q$,则 $k$ 列的行动路线形如\[ \underbrace{P\to Q\to P\to Q}_{16~\text{对}}\to \cdots \to \underbrace{Q\to P\to Q\to P\to \cdots Q\to P}_{16~\text{对}},\]因此 $k$ 列只能在区域 $M\cap P$ 和区域 $N\cap Q$ 之间移动,显然无法覆盖所有区域,命题得证.
解法可以简化为在区域 $M\cap P$(包含 $16$ 格)中的项的下一项必然在区域 $N\cap Q$(包含 $16$ 格)中,但根据移动规则,区域 $M\cap P$ 的 $16$ 格的下一个只能覆盖 $12$ 格(不包含 $(3,3),(6,3),(3,6),(6,6)$),如图.