2015年高考数学安徽卷理科第15题（填空压轴题）：
设\(x^3+ax+b=0\)，其中\(a,b\)均为实数，下列条件中，使得该三次方程仅有一个实根的是_______（写出所有正确条件的编号）．
① \(a=-3\)，\(b=-3\)；
② \(a=-3\)，\(b=2\)；
③ \(a=-3\)，\(b>2\)；
④ \(a=0\)，\(b=2\)；
⑤ \(a=1\)，\(b=2\)．
正确答案是①③④⑤．
根据题意，直线\(y=-b\)和函数\(y=x^3+ax\)的图象有且仅有一个公共点．
先考虑\(a=-3\)的情形．
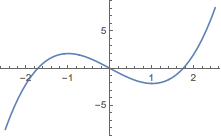
此时\(f'(x)=3x^2-3\)，于是\(f(x)\)在\(x=-1\)取得极大值\(2\)，在\(x=1\)处取得极小值\(-2\)，如图．
于是当\(b<-2\lor b>2\)时符合题意．
再考虑\(a\geqslant 0\)的情形．
此时\(f(x)\)单调递增，且值域为\(\mathcal R\)，于是必然符合题意．
综上，符合题意的答案为①③④⑤．