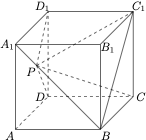
如图,在棱长为 $1$ 的正方体 $A B C D-A_{1} B_{1} C_{1} D_{1}$ 中,动点 $P$ 在线段 $A_{1} B$ 上,设 $l$ 是平面 $D D_{1} P$ 与平面 $C C_{1} P$ 的交线.
1、求证:$l\parallel C C_{1}$.
2、若 $P$ 是线段 $A_{1} B$ 上靠近 $A_{1}$ 的四等分点,求平面 $D D_{1} P$ 与平面 $C C_{1} P$ 所成二面角的正弦值.
解析
1、由于 $CC_1\parallel DD_1$ 且 $CC_1$ 不在平面 $PDD_1$ 中,因此 $CC_1\parallel PDD_1$,根据线面平行的性质定理,有 $l\parallel CC_1$.
2、将 $P$ 按 $\overrightarrow{AB}$ 平移到 $P_1$,则平面 $DD_1P$ 与平面 $CC_1P$ 所成二面角的正弦值即 $\sin\langle P-CC_1-P_1\rangle $.建立空间直角坐标系 $C-DBC_1$,不改变问题的本质,将正方体棱长重设为 $4$,有\[\begin{cases} P(3,4,3),\\ C(0,0,0),\\ C_1(0,0,4),\\ P_1(-1,4,3),\end{cases}\implies \begin{cases} \overrightarrow{PC}=(-3,-4,-3),\\ \overrightarrow{CC_1}=(0,0,4),\\ \overrightarrow{C_1P}=(-1,4,-1),\end{cases}\implies \begin{cases} \overrightarrow n_{PCC_1}=(-4,3,0),\\ \overrightarrow n_{CC_1P}=(-4,-1,0),\end{cases} \]因此\[\cos\langle P-CC_1-P_1\rangle =\dfrac{\overrightarrow n_{PCC_1}\cdot \overrightarrow n_{CC_1P_1}}{\left|\overrightarrow n_{PCC_1}\right|\cdot \left|\overrightarrow n_{CC_1P_1}\right|}=\dfrac{13}{5 \sqrt{17}},\]进而可得所求正弦值为\[\sqrt{1-\cos^2\langle P-CC_10P_1\rangle }=\dfrac{16\sqrt{17}}{85}.\]
