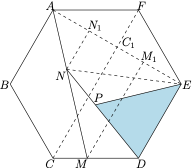
如图,正六边形 $ABCDEF$ 的面积为 $125$,且\[\dfrac{CM}{MD}=\dfrac{AN}{NM}=\dfrac{NP}{PD}=\dfrac 23,\]则 $\triangle PDE$ 的面积为_______.

答案 $18$.
解析 如图,连接 $NE,AE$,设 $N,M,C$ 在 $AE$ 上的投影分别为 $N_1,M_1,C_1$,则 $F$ 在 $AE$ 上的投影也是 $C_1$.
设 $AC_1=C_1E=5h$,则由于 $\dfrac{CM}{MD}=\dfrac 23$,可得 $C_1M_1=2h$,于是 $AM_1=7h$.又 $\dfrac{AN}{NM}=\dfrac 23$,于是\[AN_1=\dfrac 25\cdot AM_1=\dfrac{14}5h,\]从而\[N_1E=AE-AN_1=10h-\dfrac{14}5h=\dfrac{36}5h,\]因此\[[PDE]=\dfrac 35[NDE]=\dfrac 35\cdot \dfrac 12\cdot DE\cdot \dfrac{36}5h=\dfrac{108}{125}\cdot \left(\dfrac 12\cdot DE\cdot 5h\right)=\dfrac{108}{125}\cdot \dfrac{125}6=18.\]
备注 事实上,根据定比分点坐标公式有\[d(N,DE)=\dfrac{3d(A,DE)+2d(M,DE)}5=\dfrac{3\cdot 2d(C,DE)+2\cdot \dfrac 35d(C,DE)}{5}=\dfrac{36}{25}d(C,DE).\]/wp-admin/post.php?post=31252&action=edit
