每日一题[131] 极化恒等式

正方体\(ABCD-A_1B_1C_1D_1\)的棱长为\(2\)，\(MN\)是它的内切球的一条弦（我们把球面上任意两点之间的线段称为球的弦），\(P\)为正方体表面上的动点，当弦\(MN\)的长度最大时，\(\overrightarrow{PM}\cdot\overrightarrow{PN}\)的取值范围是_______．

正确的答案是\([0,2]\)．

长度最大的弦\(MN\)为直径，设内切球的球心为\(O\)．根据极化恒等式（平面向量的“积化和差”公式），有\[\begin{split}4\overrightarrow{PM}\cdot\overrightarrow{PN}&=\left(\overrightarrow{PM}+\overrightarrow{PN}\right)^2-\left(\overrightarrow{PM}-\overrightarrow{PN}\right)^2\\&=4OP^2-MN^2\\&=4OP^2-4,\end{split}\]于是\[\overrightarrow{PM}\cdot\overrightarrow{PN}=OP^2-1,\]其取值范围为\([0,2]\)．

注   根据此题可知对线段\(MN\)而言，\(\overrightarrow{PM}\cdot\overrightarrow{PN}\)为定值的点\(P\)的轨迹为球面，且\(\overrightarrow{PM}\cdot\overrightarrow{PN}\)越大，球的半径越大．于是当该球与正方体内切时\(\overrightarrow{PM}\cdot\overrightarrow{PN}\)最小，当该球与正方体外接时\(\overrightarrow{PM}\cdot\overrightarrow{PN}\)最大．

2015年9月4日补充练习题．

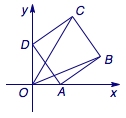
（2013年·临沂三模）如图放置的正方形\(ABCD\)，\(AB=1\)，\(A\)、\(D\)分别在\(x\)轴、\(y\)轴的正半轴（含原点）上滑动，则\(\overrightarrow{OC}\cdot\overrightarrow{OB}\)的最大值是_______．

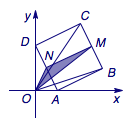
解    取\(BC\)中点\(M\)，\(AD\)中点\(N\)，则由极化恒等式\[4\vec a\cdot \vec b=\left(\vec a+\vec b\right)^2-\left(\vec a-\vec b\right)^2,\]可得\[\overrightarrow {OC}\cdot\overrightarrow {OB}=OM^2-\dfrac 14BC^2=OM^2-\dfrac 14,\]

连接\(ON\)、\(NM\)，则有\[OM\leqslant ON+NM=\dfrac 12AD+AB=\dfrac 32,\]等号当\(O\)、\(N\)、\(M\)三点共线时取得，因此\(OM\)的最大值为\(\dfrac 32\)，所求数量积的最大值为\(2\)．

2015年11月13日补充练习．

已知点$O$为坐标原点，$\triangle ABC$为圆$C_1:(x-1)^2+(y-\sqrt 3)^2=1$的内接正三角形，则$\overrightarrow {OA}\cdot\left(\overrightarrow {OB}+\overrightarrow {OC}\right)$的最小值为_______．

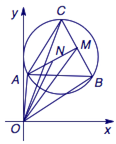
解    如图，取$BC$的中点$M$，连接$AM$，取$AM$的中点$N$．

欲求代数式$$\begin{split} \overrightarrow {OA}\cdot\left(\overrightarrow {OB}+\overrightarrow {OC}\right)&=\overrightarrow {OA}\cdot 2\overrightarrow {OM}\\&=2\left(ON^2-\dfrac 14AM^2\right)\\&=2ON^2-\dfrac12AM^2,\end{split} $$其中用到了极化恒等式$$4\overrightarrow {OA}\cdot\overrightarrow {OM}=\left(\overrightarrow{OA}+\overrightarrow{OM}\right)^2-\left(\overrightarrow {OA}-\overrightarrow {OM} \right)^2.$$

由圆$C_1$的半径为$1$可得$\triangle ABC$的边长为$\sqrt 3$，于是$$AM=\dfrac 32.$$又$$C_1N=C_1A-\dfrac 12AM=\dfrac 14,$$于是点$N$在以$C_1$为圆心，$\dfrac 14$为半径的圆上．

因此$\overrightarrow {OA}\cdot\left(\overrightarrow {OB}+\overrightarrow {OC}\right)$的最小值为$$2(OC_1-C_1N)^2-\dfrac 12AM^2=5.$$