如图，将一张边长为\(1\)的正方形纸\(ABCD\)折叠，使得点\(B\)始终落在边\(AD\)上，则折起部分面积的最小值为_______．
正确答案为\(\dfrac 38\)．
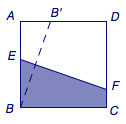
如图，设\(AB'=x(0\leqslant x\leqslant 1)\)，则由相似三角形可得\[\dfrac{BE}{BB'}=\dfrac{\frac 12BB'}{AB},\]从而\[BE=\dfrac{BB'^2}{2AB}=\dfrac 12\left(1+x^2\right),\]而继续由相似三角形可得\[\dfrac{BE-CF}{BE}=\dfrac{BC}{BG},\]从而\[BE-CF=BC\cdot\dfrac{BE}{BG}=x,\]解得\[CF=\dfrac 12\left(1+x^2\right)-x,\]因此\[\begin{split}S_{EBCF}&=\dfrac 12\left(BE+CF\right)\cdot BC\\&=\dfrac 12\left(x^2-x+1\right)\\&\geqslant \dfrac 38,\end{split}\]等号当且仅当\(x=\dfrac 12\)时取得．
注 若此题改为求线段\(EF\)划过的面积，则为中国科学技术大学（USTC）的一道自主招生题．
如图，作\(B'K\perp BC\)于\(K\)，连接\(BK\)，则不难得到\(EF\)始终与以\(B\)为焦点，直线\(AD\)为准线的抛物线相切于点\(K\)．这样我们就可以得到线段\(EF\)关于点\(B'\)形成的轨迹（Locus），如图所示．
由此，可以求得所求面积为\[1-\dfrac 38-\int_0^1{\left(\dfrac 12-\dfrac 12x^2\right)}{\mathrm d}x=\dfrac{7}{24}.\]