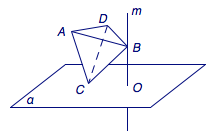
直线\(m\)与平面\(\alpha\)垂直,垂足是\(O\),正四面体\(ABCD\)的棱长为\(4\),点\(C\)在平面\(\alpha\)上运动, 点\(B\)在直线\(m\)上运动,则点\(O\)到直线\(AD\)的距离的取值范围是( )
A.\(\left[\dfrac{4\sqrt 2-5}{2},\dfrac{4\sqrt 2+5}{2}\right]\)
B.\(\left[2\sqrt 2-2,2\sqrt 2+2\right]\)
C.\(\left[\dfrac{3-2\sqrt 2}{2},\dfrac{3+2\sqrt 2}{2}\right]\)
D.\(\left[3\sqrt 2-2,3\sqrt 2+2\right]\)
问题的关键是正确的把握运动中的不变量.事实上,看起来非常复杂的\(B\)、\(C\)两个点的运动,在其运动过程中,\(OB\)与\(OC\)的垂直关系是始终不变的.因此,我们可以将正四面体\(ABCD\)固定下来,而点\(O\)在以\(BC\)为直径的球面上运动,如图.
接下来可以得到所求的点\(O\)到直线\(AD\)的距离的取值范围就是球心到直线\(AD\)的距离减去球的半径与球心到直线\(AD\)的距离加上球的半径之间,不难求出该取值范围是\(\left[2\sqrt 2-2,2\sqrt 2+2\right]\).