在半径为\(2\)的球面上有三个点\(A,B,C\),求\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)的取值范围.
考虑到连续性,只需要求出数量积的最大值和最小值即可.
先求最大值.
由于\[\begin{split}2\overrightarrow{AB}\cdot\overrightarrow{AC}&\leqslant \overrightarrow{AB}\cdot\overrightarrow{AB}+\overrightarrow{AC}\cdot\overrightarrow{AC}\\&\leqslant 4^2+4^2=32,\end{split}\]等号当且仅当\(B=C\),且\(AB\)、\(AC\)均为球的直径时取得,因此所求数量积的最大值为\(16\).
再求最小值.
若\(A\)、\(B\)、\(C\)中有重合的点,那么所求数量积为\(0\),但显然\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)可以取到负值,于是只需要考虑\(A\)、\(B\)、\(C\)中没有重合的点的情形.
此时\(A\)、\(B\)、\(C\)必然共圆,设三角形\(ABC\)的外接圆\(O\)半径为\(r\),则\(0<r\leqslant 2\).
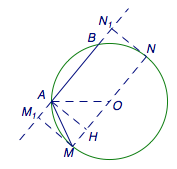
如图,使用调整法,在向量\(\overrightarrow{AB}\)确定的情况下,连接\(OA\),设\(\overrightarrow{AB}\)与\(\overrightarrow{AO}\)所成角为\(\theta\).过圆心\(O\)作\(\overrightarrow{AB}\)所在基线的平行线,被圆截得直径\(MN\),分别作\(M\)、\(N\)在基线上的投影\(M_1\)、\(N_1\),则有\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)的取值范围是\(\left[\overrightarrow{AM_1}\cdot\overrightarrow{AB},\overrightarrow{AN_1}\cdot\overrightarrow{AB}\right]\).
事实上,有\[\begin{split}\overrightarrow{AM_1}\cdot\overrightarrow{AB}&=-\left(r-r\cos\theta\right)\cdot 2r\cos\theta\\&\geqslant -\dfrac 12r^2\\&\geqslant -2,\end{split}\]等号当且仅当\(\cos\theta=\dfrac 12\land r=2\)时取得.
因此所求数量积的最小值为\(-2\).
注 本方法也可以用来求最大值.