每日一题[113] 平面向量的“积化和差”

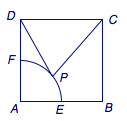
如图，已知正方形$ABCD$的边长为$2$，点$E$为$AB$的中点．以$A$为圆心，$AE$为半径，作弧交$AD$于点$F$．若$P$为劣弧$EF$上的动点，则$\overrightarrow{PC}\cdot\overrightarrow{PD}$的最小值为_______．

---

正确答案是$5-2\sqrt 5$．

坐标法

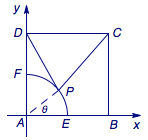
以$A$为原点，$AB$为$x$轴方向，$AD$为$y$轴方向建立平面直角坐标系，如图．

设$\angle PAE=\theta$，则$C(2,2)$、$D(0,2)$、$P\left(\cos\theta,\sin\theta\right)$，其中$\theta\in\left[0,\dfrac{\pi}{2}\right]$．

于是

$$\begin{split}\overrightarrow{PC}\cdot\overrightarrow{PD}&=\left(2-\cos\theta,2-\sin\theta\right)\cdot\left(-\cos\theta,2-\sin\theta\right)\\&=5-4\sin\theta-2\cos\theta\\&=5-2\sqrt 5\sin\left(\theta+\varphi\right)\\&\geqslant 5-2\sqrt 5,\end{split}$$ 其中$\varphi$为辅助角，等号可以取得．

因此所求最小值为$5-2\sqrt 5$．

---

“积化和差”

我们熟知极化恒等式

$$4\overrightarrow a\cdot\overrightarrow b=\left(\overrightarrow a+\overrightarrow b\right)^2-\left(\overrightarrow a-\overrightarrow b\right)^2,$$ 而注意到在本问题中向量$\overrightarrow{PC}$与向量$\overrightarrow{PD}$的差为定向量，于是 $$\begin{split}4\overrightarrow{PC}\cdot\overrightarrow{PD}&=\left(\overrightarrow{PC}+\overrightarrow{PD}\right)^2-\left(\overrightarrow{PC}-\overrightarrow{PD}\right)^2\\&=\left(\overrightarrow{PC}+\overrightarrow{PD}\right)^2-4,\end{split}$$ 取$CD$的中点$M$，则有 $$\overrightarrow{PC}\cdot\overrightarrow{PD}=PM^2-1,$$ 如图．

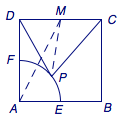
问题转化为求$PM^2-1$的最小值，显然当$A$、$P$、$M$三点共线时，$PM^2-1$取得最小值

$$\left(AM-1\right)^2-1=\left(\sqrt 5-1\right)^2-1=5-2\sqrt 5.$$