每日一题[37] 向量的正交分解

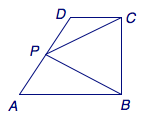
如图，在直角梯形$ABCD$中，$AB\parallel CD$，$AB\perp BC$，$AB=2$，$CD=1$，$BC=a$，$P$为线段$AD$（含端点）上的一个动点．设$\overrightarrow{AP}=x\overrightarrow{AD}$，$\overrightarrow{PB}\cdot\overrightarrow{PC}=y$，对于函数$y=f(x)$，给出以下三个结论：

① $\forall a\in (0,+\infty)$，都有$f(1)=1$成立；

② $\forall a\in (0,+\infty)$，函数$f(x)$的最大值都等于$4$；

③ 当$a=2$时，$f(x)$的值域为$[1,4]$．

所有正确结论的序号是_______．

---

 答案是①②．

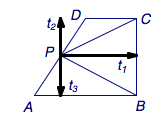
如图，将$\overrightarrow{PB}$、$\overrightarrow{PC}$正交分解，则有

$$\begin{split}\overrightarrow{PB}\cdot\overrightarrow{PC}&=\left(\overrightarrow{t_1}+\overrightarrow{t_3}\right)\cdot\left(\overrightarrow{t_1}+\overrightarrow{t_2}\right)\\&=\overrightarrow{t_1}\cdot\overrightarrow{t_1}+\overrightarrow{t_2}\cdot\overrightarrow{t_3}\\&=(2-x)^2-a^2x(1-x).\end{split}$$

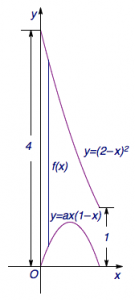
此时容易知道①②正确，如图．

考虑③，当$a=2$时，由上式

$$f(x)=5x^2-8x+4,$$ 当$x\in [0,1]$时，其值域为$\left[\dfrac 45,2\right]$．

事实上，只有$a\leqslant\sqrt 2$时，函数$f(x)$的值域才为$[1,4]$．

---

 点评    正交分解是处理向量问题，尤其是数量积的问题的重要方法．但此题的最好解法为利用极化恒等式，可以参考http://lanqi.org/?p=2647及http://lanqi.org/?p=2965．