已知非零向量\(\overrightarrow a\)和\(\overrightarrow b\)互相垂直，则\(\overrightarrow a+ \overrightarrow b\)和\(\overrightarrow a+2\overrightarrow b\)的夹角余弦值的最小值为_______．
正确的答案是\(\dfrac{2\sqrt 2}{3}\)．
法一
根据题意，所求两个向量夹角的余弦值为\[\begin{split}\dfrac{\left(\overrightarrow a+\overrightarrow b\right)\cdot\left(\overrightarrow a+2\overrightarrow b\right)}{\left|\overrightarrow a+\overrightarrow b\right|\cdot\left|\overrightarrow a+2\overrightarrow b\right|}&\triangleq \dfrac{x+2y}{\sqrt{x+y}\cdot\sqrt{x+4y}}\\&=\sqrt{\dfrac{x^2+4xy+4y^2}{x^2+5xy+4y^2}}\\&= \sqrt{1-\dfrac{xy}{x^2+5xy+4y^2}}\\&=\sqrt{1-\dfrac{1}{\dfrac xy+4\cdot\dfrac yx+5}}\\&\geqslant\sqrt{1-\dfrac{1}{9}}\\&=\dfrac{2\sqrt 2}{3},\end{split}\]其中\(\overrightarrow a\cdot \overrightarrow a =x\)，\(\overrightarrow b\cdot \overrightarrow b=y\)，等号当且仅当\(x=2y\)时取得．
法二
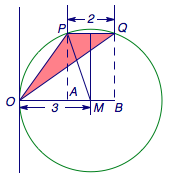
如图，设\(\overrightarrow {OA}=\overrightarrow {AB}=\overrightarrow b\)，\(\overrightarrow{OP}=\overrightarrow a+\overrightarrow b\)，\(\overrightarrow{OQ}=\overrightarrow a+2\overrightarrow b\)，且\(OA=AB=2\)，取线段\(AB\)的中点\(M\)．
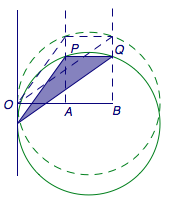
由圆的等张角性可知，当三角形\(OPQ\)的外接圆与\(\overrightarrow a\)的基线相切于\(O\)点时\(\angle POQ\)最大，此时容易求得\[\cos\angle POQ=\dfrac{\sqrt{PM^2-\left(\dfrac 12PQ\right)^2}}{PM}=\dfrac{2\sqrt2}{3}.\]否则当线段\(PQ\)上下平移时，\(O\)点在圆的外部，对应的张角\(\angle POQ\)会变小，如图．
