设函数 \(f(x)=kx^2-kx\)，\(g(x)=\begin{cases} \ln x,&x\geqslant 1,\\ -x^3+(a+1)x^2-ax,&0<x<1,\end{cases}\) 若使得不等式 \(f(x)\geqslant g(x)\) 对一切正实数 \(x\) 恒成立的实数 \(k\) 存在且唯一，则实数 \(a\) 的值为_______．
正确答案是\(2\)．
分析与解 根据题意，有\[\forall 0<x<1,k(x-1)\geqslant -x^2+(a+1)x-a,\]且\[\forall x>1,k(x-1)\geqslant \dfrac{\ln x}x.\]如图，若使得不等式 \(f(x)\geqslant g(x)\) 对一切正实数 \(x\) 恒成立的实数 \(k\) 存在且唯一，则直线 \(y=k(x-1)\) 是函数\[\begin{split} g_1(x)&=\dfrac{\ln x}x,\\g_2(x)&=-x^2+(a+1)x-a\end{split}\]的公切线．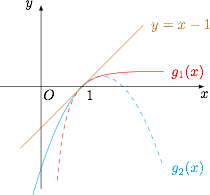
因此\[\left(\dfrac{\ln x}x\right)'_{x=1}=\left(-x^2+(a+1)x-a\right)'_{x=1},\]也即\[1=-2+(a+1),\]解得 \(a=2\)．